.
asdf: rozwiąż
xcosx − sinx = 0
wyszło mi:
x = tgx
jak dalej?
3 lut 18:46
asdf: x=0?
3 lut 18:47
Basia:
x = tgx ⇔ x=0
ale gdzie przypadek cosx=0 ?
3 lut 18:49
asdf: x=2kπ?
3 lut 18:50
Basia:
nie.......................
dla cosx = 0 masz
x*0 − sinx = 0
−sinx = 0
sinx = 0
a to jest niemożliwe
czyli zostaje tylko x=0
ale trzeba to napisać i to "niemożliwe" uzasadnić
3 lut 18:54
asdf: a...ok

3 lut 18:56
pigor: ... zrób sobie wykresy y=x i y=tgx i w x=0 jedyny ich punkt wspólny . ...

3 lut 18:57
asdf: @właśnie tak robiłem
3 lut 18:57
ICSP: Basiu nie podoba mi się stwierdzenie :
tgx = x ⇔ x = 0
Jak dla mnie to oczywista nieprawda
3 lut 19:01
Basia:
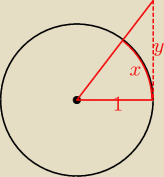
to jak myślisz kiedy y=x ?
3 lut 19:04
Basia: w przedziale (−π2; π2) oczywiście
zapomniałam dopisać
3 lut 19:06
Mila:
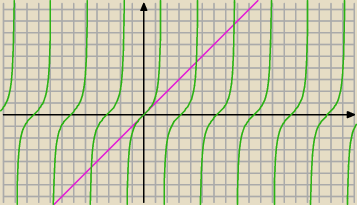
3 lut 19:09
asdf: no tak, zrobiłem tak samo jak Mila, dlatego nie sprawdzalem dla cosx.
3 lut 19:11
Mila:
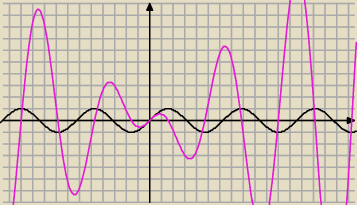
To są wykresy
y=xcosx
y=sinx
Na YAHOO jest dyskusja na temat tego równania, ale słabo znam angielski.
Ciekawe.
3 lut 19:36




 To są wykresy
y=xcosx
y=sinx
Na YAHOO jest dyskusja na temat tego równania, ale słabo znam angielski.
Ciekawe.
To są wykresy
y=xcosx
y=sinx
Na YAHOO jest dyskusja na temat tego równania, ale słabo znam angielski.
Ciekawe.