Olimpiada AGH Kamcio :): Dzisiaj odbył się II Etap olimpiady o diamentowy indeks AGH wrzucam zadania jakby ktoś chciał się pobawić: Po 10 pkt: 1) Rozwiąż równanie (5√2−7)^x−1=(5√2+7)^3x 2)Jedna z krawędzi bocznych ostrosłupa jest prostopadła do jego podstawy, będącej prostokątem o bokach długości 5cm i 12cm. Najdłuższa krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60⁰. Oblicz pole powierzchni bocznej ostrosłupa. 3) Wyznacz dziedzinę funkcji określonej wzorem f(x)=√log_¹π(2x−1)−log_¹π(5−3x) 4) Oblicz granicę ciągu (a_n) gdzie

	3+6+9+...+3n
an=
	(2n+1)2

Zadania po 20pkt: 5)Wykaż , że (2n+2)−cyfrowa liczba 11....122.....25 (jedynek jest n, dwójek n+1 a piątka jedna) jest kwadratem liczby naturalnej (dla dowolnego n) 6) Dane są punkty A=(−5,0) B=(−3,−4) C=(3,4) M=(7,1). Z punktu M poprowadzono styczne k i l do okręgu opisanego na trójkacie ABC. Oblicz pole trójkąta KLM , gdzie K i L są punktami styczności prostych k i l z okręgiem. 7)Rzucamy monetą n razy (n≥2). Oblicz prawdopodobieństwo zdarzeń: A:reszka wypadła dokładnie k razy; B: Reszka wypadła więcej razy niż orzeł; C: przynajmniej dwa razy pod rząd moneta upadła tą samą stroną Miłego rozwiązywania, moim zdaniem zadania były trudne jak na poziom tej olimpiady, aczkolwiek dało się większość z nich zrobić

3: poprawka: podstawą logarytmu było (π −1). pzdr

Prośba : Mógłby ktoś rozwiązać zadanie 5?

Kamcio :): π⁻¹ na 100%, w mojej sali padło takie pytanie i odpowiedź członka komisji była π⁻¹

Kamcio :): Ja zrobiłem tak: 5) Liczbę tą możemy zapisać w systemie dziesiętnym w postaci: 10²ⁿ⁺²+10²ⁿ⁺¹+...+10ⁿ⁺²+2(10ⁿ⁺¹+10ⁿ+...+10)+5= (ze wzoru na sumę ciągu geometrycznego) =

	1−10n		1−10n+1		102n+2−10n+2+2*10n+2+25
10n+2*		+2*10		+5=		=
	1−10		1−10		9

	102(n+1)+10*10n+1+25		10n+1+5
		=(		)2
	9		3

Widzimy teraz że dana liczba jest kwadratem pewnej liczby, teraz tylko wystarczy dowieść że ten ułamek w nawiasie jest naturalny, czyli że licznik dzieli się przez 3. Jak wiemy z cech podzielności przez 3 liczba dzieli się przez 3, jeżeli suma jej cyfr dzieli się przez 3. W liczniku mamy liczbę postaci 100...05 Widzimy że suma jej cyfr wynosi 6 dla dowolnego n, 3|6, a więc dana liczba jest kwadratem pewnej liczby naturalnej c.n.w

lelol: małuża

oti: kiedy będą wyniki ? wie ktoś może ?

Kamcio :): prawdopodobnie w ciągu około 2−3 tygodni

Nienor: Widziałam was, jak szukałam sali Przynajmniej tych co mieli w A4, nie wiem czy wszyscy tam mieli Więc pierwsze:

	1		5√2−7
(5√2+7)−1=		=		=5√2−7
	5√2+7		2*25−49

Z:5√2−7=t

	1
tx−1=(		)3x
	t

t^x−1=t^−3x x−1=−3x (bo t^x jest funkcją różnowartościową) 4x=1

	1
x=
	4

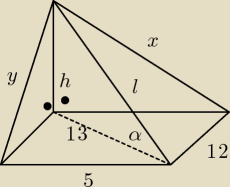
Nienor: Skąd się wzięła 13, tłumaczyć chyba nie muszę

	h
tg60o=√3=		⇒ h=13√3
	13

	1		13
cos60o=		=		⇒ h=26
	2		h

x²=(13√3)²+5²=507+25=532 x=2√133 y²=(13√3)²+12²=507+144=651 y=√651 Trójkąt z 5 i y jest prostokątny: 26²=676 y²+5²=651+25=676 Trójkąt z 12 i x jest prostokątny: 144+x²=144+532=676

	1		1
Pb=		(5y+5x+12y+12x)=		(60√651+120√133=30√651+60√133
	2		2

Nienor: 1.

	1
log1π(2x−1)−log		(5−3x)≥0
	π

	2x−1
log1π		≥0
	−3x+5

2x−1		1
	≤1, bo		<1, więc funkcja log1πx jest malejąca
−3x+5		π

2x−1+3x−5
	≤0
−3x+5

(5x−6)(−3x+5)≤0

	6		5
(x−		)(x−		)≥0
	5		3

	1
2. 2x−1>0 ⇔ x>
	2

2x−1≠1 ⇔ x≠1

	5
3.−3x+5>0 ⇔ x<
	3

	4
−3x+5≠1 ⇔ x≠
	3

Zsumować wszystkie wyniki:

	1		6
Df(x)=(		;		)
	2		5

Nienor: licznik suma ciągu arytmetycznego o pierwszym wyrazie 3 i różnicy 3

	1		1		3		3
Sn=		(3+3+3(n−1))n=		(3+3n)n=		n2+		n
	2		2		2		2

	32n2+32n		32+32n
lim		=lim
	4n2+8n+1		4+8n+1n2

	32		3
=		=
	4		8

poeta: weszłam tutaj przez przypadek ale stwierdzam ze wasza wiedza jest ogromna ale nie popadajcie w zaszczytach tylko róbcie dalej to co lubicie, i skromność sie przy tym też opłaci a swiat czeka na was otworem

Mila: Świat nas wynagrodzi "magicznym domem" . Kto dzisiaj ceni wiedzę? I co nam ta wiedza da?

poeta: satysfakcje ... to też dużo ja bardzo cenie wiedze, choć z przykrością stwierdzam, że ludzie sie jej wypieraja twierdzac ze nic nie umieją, każdy przecież coś umie, a to już jakaś wiedza. im wieksza, tym wieksza satysfakcja. lecz trzeba pamietac o waznych słowach " wiem, że nic nie wiem "

poeta: Jeśli istnieje na świecie człowiek,który ma najwiekszy iloraz inteligencji to trzeba z przykroscia stwierdzic , myslac filozoficznie, że i tak nic nie umie. Nic a jednak coś, coś a jednak nic .... przepraszam za te wywody moje, ale o tej porze nuruja mnie tematy egzystencjonalne