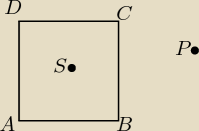
 Dany jest kwadrat ABCD o środku w punkcie S i punkt P − jak na rysunku. Udowodnij, ze suma
kwadratów odległośći punktu P od wierzchołków A,B,C i D jest równa 4|PS|2 + |AC|2
Licze na pomoc
Dany jest kwadrat ABCD o środku w punkcie S i punkt P − jak na rysunku. Udowodnij, ze suma
kwadratów odległośći punktu P od wierzchołków A,B,C i D jest równa 4|PS|2 + |AC|2
Licze na pomoc

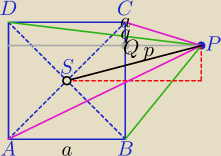 1)| PC|2+|PA|2=|PB|2+|PD|2
L=q2+p2+(a+p)2+(a−q)2
P=(a−q)2+p2+(a+p)2+q2
L=P=2a2+2ap−2aq+2p2+2q2
2)
1)| PC|2+|PA|2=|PB|2+|PD|2
L=q2+p2+(a+p)2+(a−q)2
P=(a−q)2+p2+(a+p)2+q2
L=P=2a2+2ap−2aq+2p2+2q2
2)
| a | a | a2 | ||||
|PS|2=( | +p)2+( | −q)2= | +ap+p2−aq+q2 | |||
| 2 | 2 | 2 |
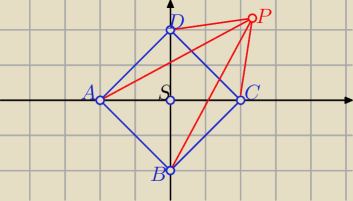 A(−a,0) , B(0,−a) , C(a,0) , D(0,a) , P(x,y) i |AC|2=(2a)2=4a2 |PS|2=x2+y2
|PC|2=(x−a)2+y2
|PD|2=x2+(y−a)2
|PA|2=(x+a)2+y2
|PB|2=x2+(y+a2)
+ −−−−−−−−−−−−−−−−−−−−−−−
= 4x2+4y2 +4a2 = 4|PS}=|AC|2
A(−a,0) , B(0,−a) , C(a,0) , D(0,a) , P(x,y) i |AC|2=(2a)2=4a2 |PS|2=x2+y2
|PC|2=(x−a)2+y2
|PD|2=x2+(y−a)2
|PA|2=(x+a)2+y2
|PB|2=x2+(y+a2)
+ −−−−−−−−−−−−−−−−−−−−−−−
= 4x2+4y2 +4a2 = 4|PS}=|AC|2
 =4|PS|2+|AC|2
=4|PS|2+|AC|2
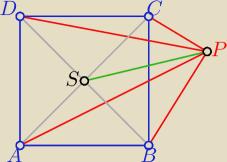 2 sposób
ze wzoru na długość środkowej PS
w ΔAPC
4|PS|2=2|PC|2+2|PA|2−|AC|2
i w ΔBPC
4|PS|2=2|PD|2+2|PB|2− |BD|2 , |BD|2=|AC|2
dodając stronami i dzieląc równość przez 2 otrzymamy tezę
2 sposób
ze wzoru na długość środkowej PS
w ΔAPC
4|PS|2=2|PC|2+2|PA|2−|AC|2
i w ΔBPC
4|PS|2=2|PD|2+2|PB|2− |BD|2 , |BD|2=|AC|2
dodając stronami i dzieląc równość przez 2 otrzymamy tezę