geometria analityczna Marcin: Sieczna x −7y +5= 0 przecina okrąg x²+y²−12x+4y+15=0 w punktach A i B, w których przeprowadzono styczne przecinające się w punkcie C. Obliczyć pole trójkąta ABC.

Artur_z_miasta_Neptuna: rysunek chociaż zrobiony wyznaczony środek i promień okręgu wyznaczone punkty przecięcia siecznej z okręgiem

Marcin: Tak to mam zrobione S(6,−2) r=5 punkty A=(2,1) B=(9,2) ale nie wiem co dalej..

Artur_z_miasta_Neptuna: jak się wyznacza proste styczne do okręgu w punkcie A=(x₀,y₀)

Marcin: Mam napisać równanie prostej prostopadłej w punkcie A?

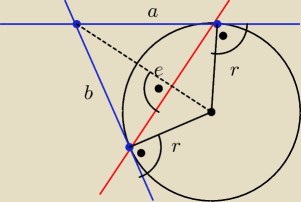
Artur_z_miasta_Neptuna: z powyższego rysunku wynika, że trójkąt ABC jest równoramienny, a wysokość tego trojkąta zawiera się w prostopadłej do tej siecznej. musisz tylko ładnie to opisać i wyznaczyć przynajmniej jedną z stycznych (w celu wyznaczenia punktu C jako przecięcia wysokości i jednego z boków trojkata

Marcin: Ok. Dzięki za pomoc spróbuje to rozwiązać

Marcin: coś mi nie wychodzi... obliczyłem środkową boku AB, D=(5,5;1,5) napisałem równanie prostopadłej do siecznej przechodzącej przez punkt D i wyszło mi coś takiego y=−7x+40 obliczyłem też długość odcinka AB=5√2 i stanąłem w miejscu...i nie wiem teraz jak wyznaczyć ten punkt C?

Artur_z_miasta_Neptuna: jeszcze raz ci napiszę −−− wyznaczyć musisz STYCZNĄ do okręgu w punkcie A lub B ... przecięcie tej prostej i środkowej, która wyznaczyleś da Ci punkt C sprawdź czy srodkowa przechodzi przez środek okręgu

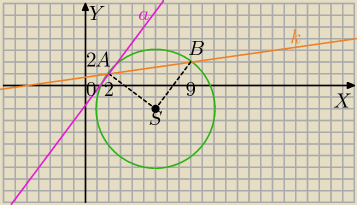
Mila: prosta k: x−7y+5=0 okrąg: (x−6)²+(y+2)²=5² styczna a: y=ax+b i A=(2;1)∊A i a⊥SA 1=2a+b ⇔b=1−2a a: y=ax+1−2a ⇔ax−y+1−2a=0 odległość punktu S=(6;−2) od prostej a jest równa 5.

|6a+2+1−2a|
	=5⇔|4a+3|=5√a2+1 /2
√a2+1

po podniesieniu do kwadratu i uporządkowaniu: 9a²−24a+16=0 Δ=0

	24		4
a=		=
	18		3

styczna a:

	4		4		4		5
y=		x+1−2*		⇔y=		x−		x
	3		3		3		3

Z drugą styczną podobnie

Marcin: Dzięki ogromneteraz właśnie obliczyłem tę styczną wynik mam taki sam

Mila: