a
szopenak:
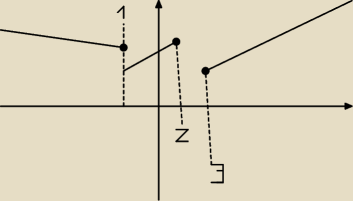
czy dana funkcja, posiada estremum w pkt 3 i 2?
czy posiada je w pkt 1?
3 lut 14:29
3 lut 14:44
Artur_z_miasta_Neptuna:
1 punkt odpada (pierwszy punkt założeń)
3 lut 14:45
Artur_z_miasta_Neptuna:
punkty 2 i 3 odpadają ze wzgledu na dziedzine (patrz pierwszy warunek)
3 lut 14:46
szopenak: no wiem wiem... że funkcja w otoczeniu Xo, nie ma wartosci większej/mniejszej od f(Xo)
Ale kurcze, skoro w pkt 3 nie ma otoczenia lewostronnego? To znaczy, że nie istnieje ekstremum,
tak to rozumiem.
a co z pkt 1? f nie jest ciągła w tym punkcie, tak więc już sam nie wiem.
Istnieje w ogóle otoczenie pkt 1?
3 lut 14:49
alfa:
Funkcja przyjmuje w punkcie x0 maksimum lokalne (odpowiednio: minimum lokalne),
jeśli w pewnym otwartym otoczeniu tego punktu (np. w pewnym przedziale otwartym) funkcja
nigdzie nie ma wartości większych (odpowiednio: mniejszych).
A może jest tak:
W 1 w otoczeniu punktu są wartości mniejsze z prawej strony i większe z lewej strony,
brak ekstremum.
W 2 w otoczeniu punktu nie ma wartości większych, więc jest maksimum.
W 3 w otoczeniu punktu nie ma wartości mniejszych, więc jest minimum.
3 lut 14:54
Artur_z_miasta_Neptuna:
alfa ... w punkcie 2 i 3 funkcja nie przyjmuje wartości w otoczeniu tychże punktów −> brak
ekstremum
przykład:
f(x) =
√x ... czy funkcja posiada ekstremum (minimum) dla x=0
3 lut 15:04
alfa:
jesteś pewien Artur? czy tylko tak Ci się zdaje
3 lut 15:06
szopenak: funkcja w 2 i 3 posiada w ogóle otoczenie ? Bo jeśli nie , to już bym to rozumiał
Tak samo w przypadku
√x w 0...
3 lut 15:08
Artur_z_miasta_Neptuna:
definicja mówi o otoczeniu
otoczenie natomiast definiowana jest jako kula o środku w x0 i promieniu ε
a kula w R1 to nic innego jak odcinek otwarty (xo − ε, x0 + ε) ... a na takim odcinku dla
x0 = 2 i x0 = 3 funkcja nie jest określona ... sprzeczność
3 lut 15:09
szopenak: wydaje mi się, ze to co mówi Artur ma sens
3 lut 15:14
szopenak: a wiec w przypadku √x w x=0 f nie ma esktremum (bo nie istnieje otoczenie).
a czy przy x=0 f jest ciągła? z def. patrząc wydaje mi się, że jest... ale nie mam pewności
3 lut 15:17
3 lut 15:20
Artur_z_miasta_Neptuna:
szopenak ... ciąglość funkcji rozpatruje się w przedzialach otwartych (tak samo jak
różniczkowalność)
czyli f(x)=√x jest ciągla na przedziale (0,+∞)
aby funkcja była ciągła w x0=0, to by musiała posiadać otoczenie w punkcie x0 ... aby możliwe
było wyliczenie granic lewo i prawo stronnych i sprawdzenie, czy są one sobie równe
brak otoczenia => brak przynajmniej jednej granicy jednostronnej => granice jednostronne nie są
równe => brak granicy w punkcie x0=0 => funkcja f(x) = √x nie jest ciągła w punkcie x0=0
3 lut 15:22
szopenak: dziękuje bardzo
mam wrażenie że rozumiem
3 lut 15:25