Letnia szkoła matematyczna Bogdan: W okresie wakacyjnym niewiele jest umieszczanych zadań na naszym forum. Zapraszam więc wszystkich rozwiązywaczy i każdego spragnionego zadań do umieszczania tutaj swoich zadań. Będziemy je wszyscy rozwiązywali dla własnej przyjemności i z pożytkiem dla wszystkich forumowiczów, szczególnie tych uczących się. To byłaby taka wakacyjna letnia szkoła matematyczna. Na początek zamieszczam, jak sądzę niezbyt trudne, 4 zadanka na dowodzenie. To nie bardzo lubiana przez uczniów forma zadań, warto więc kilka przykładów tu umieścić i pokazać, że nie taki diabeł straszny. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Udowodnij, że dla n ∊ ℕ₊ : 1. 10|n⁵ − n, (zapis ten czytamy: liczba 10 jest dzielnikiem wyrażenia n⁵ − n). 2. n! > 2ⁿ dla n ≥ 4. 3. nⁿ⁺¹ > (n + 1)ⁿ dla n > 2. 4. 37⁵⁰⁰ − 37¹⁰⁰ jest wielokrotnością 10. Zapraszam wszystkich do rozwiązywania i życzę miłej zabawy.

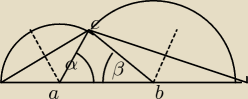
AS: Zbudować konstrukcyjnie trójkąt mając dane: obwód trójkąta i jego dwa kąty wewnętrzne.

sylwia gdańsk: sprobuje

sylwia gdańsk:

Bogdan: A jak Sylwio na prostej o długości równej obwodowi trójkąta wyznaczyłaś punkty zgięcia?

tim: Co do 1) 4) czyli ma wyjść, że to jest 1000 ... 000 ?

tim: Tzn 4) bo 1) że ma mieć na końcu 0 :?

Bogdan: Tim, wyraź się jaśniej.

Miś: zad1/ rozkładając na czynniki: n⁵ − n = n( n⁴ −1) = n( n−1)( n+1)( n²+1)= = ( n−1)*n*( n+1)*( n²+1) = ...... iloczyn trzech kolejnych liczb naturalnych jest podzielny przez 2 ( będziemy to mieć na uwadze w dalszej części dowodu) należy zatem jeszcze wykazać ,że cały ten iloczyn jest jeszcze podzielny przez 5 można dokonać takiego przekształcenia: n² +1 = n² +5 −4 zatem: (n −1)*n*(n+1)*( n² −4) + ( n−1)*(n*( n+1)* 5= (n −1)*n *(n+1)*( n−2)*(n+2) +5*(n −1)*n*(n+1)= (n −2)*(n −1)*n*( n+1)*(n+2) + 5*( n−1)*n*( n+1) pierwszy składnik jest iloczynem pięciu kolejnych liczb naturalnych więc jest podzielny przez 10 drugi składnik na tej samej zasadzie też jest podzielny przez 10 zatem 10 jest dzielnikiem n⁵ − n dla n€N₊ c.b.d.o

tim: Chodzi, mi, czy w 4) mamy udowodnić, że 37⁵⁰⁰ − 37¹⁰⁰ = 1000 ... 000

Miś: Timuś

Bogdan: Ok Misiu. Proponuję znaleźć jeszcze inny sposób wykazania prawdziwości wyrażenia: 10|n⁵ − n.

Bogdan: Tim, a co to znaczy, że jakaś liczba jest wielokrotnością liczby 10 ?

Miś: Można też wykazać: −−−− indukcyjnie −−−− lub wykazać podzielność przez 5 ( bo przez 2 jest podzielna) z rozkładu : ( n−1)*n( n+1)*(n²+1) Dam się też wykazać Innym

Bogdan: Tak, tak Misiu, pytanie o inne sposoby skierowałem do innych.

AS: n 0 1 2 3 4 5 6 7 8 9 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− n⁵ 0 1 32 243 1024 3125 7776 16807 32768 59049 Piąta potęga każdej liczby kończy się taką samą cyfrą jaka się znajduje na ostatnim miejscu tej liczby. Stąd wniosek: różnica n⁵ − n musi kończyć się zerem czyli jest podzielna przez 10

Miś:

AS: zad 3. nⁿ⁺¹ > (n + 1)ⁿ dla n > 2 n*nⁿ > (n + 1)ⁿ |:nⁿ n > (1 + 1/n)ⁿ lim_n→∞n > lim_n→∞(1 + 1/n)ⁿ ∞ > e c.n.d.

Bogdan: As,

Miś: Szkoda, że nie chciało mi się pisać rozwiązania! Dostałabym brawa

AS: Uff! Ależ zazdrośnica.

tim: Miś ... Rozumiem, że w czwartym o to hcodzi?

Miś: AS..... gdyby o Ciebie chodziło?. to ja użyłabym zdecydowanie łagodniejszego określenia

Miś: 4/ 37¹⁰⁰( 37⁴⁰⁰− 1) cyfrą jedności liczby 37⁴⁰⁰ jest 1 więc liczba 37⁴⁰⁰ −1 jest podzielna przez 10 zatem jest postaci 10*k więc : 37¹⁰⁰*(37⁴⁰⁰−1) = 10*k

Andrzej: zad. 4 rozwiązanie za pomocą kongruencji hmmm tylko nie widzę symbolu przystawania (trzy poziome kreseczki)... umówmy się zatem że zastąpię go symbolem ∼ 37⁴ ∼ 1 (mod 10) 37¹⁰⁰ = (37⁴)²⁵ ∼ 1²⁵ = 1 (mod 100) 37⁵⁰⁰ = (37⁴)¹²⁵ ∼ 1¹²⁵ = 1 (mod 100) 37⁵⁰⁰ − 37¹⁰⁰ ∼ 0 (mod 10)

Miś: OK

Bogdan: Misiu i Andrzeju Można również powiązać zadanie 4 z zadaniem 1 przyjmując n = 37¹⁰⁰: (37¹⁰⁰)⁵ − (37¹⁰⁰)

Miś: Fakt...... nie załapałam tego n⁵ − n ........ wrrrrrrr

Miś: zad2/ n! > 2ⁿ dla n≥4

	2n
		< 1
	n!

	16
dla n= 4		= 23 <1
	24

	32
n= 5		<1
	120

	2n
lim		= 0 dla n≥4 więc 0<1
	n!

n→∞ PS: Miłych snów! Dobranoc

AS: Do Miś Już nie gniewaj się tak mocno.

AS: 37⁵⁰⁰ − 37¹⁰⁰ = 37¹⁰⁰*(37⁴⁰⁰ − 1) 37⁴⁰⁰ = (37⁴)¹⁰⁰ 37⁴ = 37²*37² = (..9)*(..9) = ...1 (37⁴)¹⁰⁰ = (..1)*(..1)*...*(...1) = ...1 Wobec tego (37⁴)¹⁰⁰ − 1 musi kończyć się zerem czyli jest podzielna przez 10

tim: Mam problem, bo nie wiem czy zrozumiałem że chodzi o WIELOKROTNOŚĆ 10 (czyli 10^k), a nie jest podzielna przez 10...

AS: Nowa propozycja do łamania głowy. Zbudować konstrukcyjnie trapez mając dane podstawy i obie przekątne.

sylwia gdańsk: hm jak to zrobic jak masz przekatne to i boki wszytskie chyba

AS: Nie bardzo widzę żeby wszystkie boki były dane. A jeżeli twierdzisz że są dane to zbuduj trapez i po sprawie.

sylwia gdańsk: a sory przekatne moga byc chyba pod roznym katem nei wiem jak to ma byc ehhe

AS: Trochę odczekam − rozwiązania podam później.

tim: Czy dobrze zrozumiałem? Mam dane podstawę (a) oraz przekątne (b i c) ?

AS: Obie podstawy i dwie przekątne.

tim: Może tak: I teraz rysujemy te półkola dalej.. (Czerwone zi zielone) i rysujemy odcinek dugiej podstawy i szukamy gdzie się wpasuje Zapewne jest inna lepsza metoda.

AS: Nie jestem przekonany o poprawności konstrukcji

tim: Tzn przekątne będą miały szukaną długość, gorzej jak wpasowąć drugą podstawę.

Andrzej: Metoda "szukamy gdzie się wpasuje" to nigdy nie jest poprawna metoda konstrukcji

tim: oj wiem ...

Grażynka : Wy wszyscy robicie to źle Mój chłopak to umi rozwiązać!

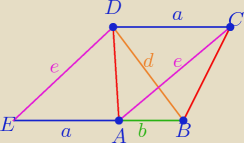
Miś: Witam 1/krok : konstruuję trójkąt o podstawie równej sumie obydwu podstaw trapezu IEBI= a + b i bokach e=IEDI i d= IBDI równych długości przekątnych ( otrzymyję ten trójkąt EBD) 2/krok : wykreślam równoległobok EACD o boku długości a jednej z podstaw trapezu i o długości drugiego boku = edługości jednej z przekątnych tego trapezu. Teraz już chyba widać ten trapez ABCD

Miś: Timuś i jak Ci się podoba ta konstrukcja ?

Miś: Oczywiście cyrklem odmierzać te zadane długości .... ale to już banał

AS: Gratulacje dla Misia

AS: Następny problem Uzasadnić cechę podzielności przez a) 4 b) 8

tim: Pięknie Misiu Pysiu

Miś: Timuś ..jak Twoje świadectwo szkolne? Myślę ,że masz same oceny celujące ?

tim: Dopiero jutro ... dziś tylko 3 GIM ... za szybko ciut

Eta: Zad/ Wnuczek ma tyle miesięcy co babcia lat. Dziadek jest starszy od babci o 4 lata. Wszyscy razem mają 129 lat. Po ile lat mają dziadkowie ? czy wnuczek jest pełnoletni?

Eta: Timuś ...... to dla Ciebie ( banalne)

tim:

	x
wnuczek =
	12

babcia = x dziadek = x + 4

	x
x + 4 + x +		= 129
	12

	x
2x +		= 125
	12

x = 60 wnuczek = 5 babcia = 60 dziakde = 64

tim: Wiem Proste Z wnuczkiem nie można iść jeszcze na piwko xD

Andrzej: To i ja dam zadanko... oczywiście dla amatorów, bo dla zawodowców to żaden problem. Najpierw definicja: Liczbą doskonałą nazywamy taką liczbę naturalną, która jest równa sumie wszystkich swoich dzielników niewłaściwych (np. liczbą doskonałymi są: 6, bo 6 = 1 + 2 + 3 oraz 28, bo 28 = 1 + 2 + 4 + 7 + 14 ). Znajdź liczbę doskonałą która jest podzielna przez 16 i ma dokładnie 10 dzielników.

Mariusz: czy chodzi o 512

Andrzej: po pierwsze: nie po drugie: to nie ma być zgadywanka, proszę o jakieś rozwiązanie

Eta: Witam pierwsza liczba doskonała : 6 druga 28 trzecia ( o którą pyta Andrzej wprawdzie tę liczbę doskonałą podał Euklides dawno , dawno temu jest nią 496 liczby doskonałe są liczbami parzystymi 496 = 1 +2 +4+8+16 +31 + 62 +124 +248 mamy dziewięć dzielników + dzielnik przez samą siebie ( czyli 10 −− dzielników) 496 = 16*31 −−−−− podzielna przez 16 jest to liczba postaci: 2^k−1* (2^k −1) gdzie 2^k − 1 −−−− jest liczbą pierwszą dla k= 5 mamy: 2⁴* (2⁵ −1)= 16 * 31 ( 31 −−− liczba pierwsza następna jako czwarta liczba doskonała to 8 128 dla zainteresowanych :liczby doskonałe kończą się cyfrą na przemian 6 i 8 uzasadnienie podobnie jak wyżej

Eta: Tak można by jeszcze pisać i pisać , całą historię tej ciekawej liczby Miłych snów ..... pozdrawiam misiowo

Eta: Dodam takie zadanko wykazać ,że liczba postaci : 10ⁿ +4ⁿ − 2 jest podzielna przez 3 dla n€N PS: zadanko do rozwiązania przez młodzież w ramach treningu wakacyjnego

Eta: Pomyślałam prostszy sposób n −−− szukana liczba doskonała skoro jest podzielna przez 16 i ma 10 podzielników to nimi są: n, 1, ⁿ₂, 2, ⁿ₄, 4 , ⁿ₈, 8, ⁿ₁₆, 16 zatem: z def. liczby doskonałej mamy: 1 + ⁿ₂ +2 + ⁿ₄ +4 + ⁿ₈ +8 + ⁿ₁₆ +16 = n

	8 +4 +2 +1
31+		*n= n
	16

n − ¹⁵₁₆*n = 31 ⁿ₁₆= 31 to: n= 31*16 n= 496 Fajnie?

AS: wykazać ,że liczba postaci : 10ⁿ +4ⁿ − 2 jest podzielna przez 3 dla n€N Rozwiązanie: A = 10ⁿ = (9 + 1)ⁿ = 9ⁿ + (n po 1)*9ⁿ⁻¹ + ... + 1 B = 4ⁿ = (3 + 1)ⁿ = 3ⁿ + (n po 1)*3*{n−1} + ... + 1 A + B − 2 = 9ⁿ + (n po 1)*9ⁿ⁻¹ + ... + 3ⁿ + (n po 1)*3ⁿ⁻¹ + ... Ostatnia suma jest podzielna przez 3 gdyż każdy składnik sumy jest podzielny przez 3 q.e.d.

Miś: Witam AS ! można też tak:( podobnie) ze wzoru: aⁿ − bⁿ= ( a−b)( aⁿ⁻¹+ aⁿ⁻²*b +.... + bⁿ⁻¹) 10ⁿ +4ⁿ −2= ( 10ⁿ −1) + ( 4ⁿ −1) = = ( 10 −1)( 10ⁿ⁻¹ + 10ⁿ⁻² +.... +1) + ( 4 −1)( 4ⁿ⁻¹ + 4^{n −2} + .... +1) = 9*( 10ⁿ⁻¹ + ..... +1) + 3*( 4ⁿ⁻¹ + .... +1) zatem jest podzielna przez 3 c.b.d.o.

AS: Dziękuję Miś. Jestem bogatszy!

Miś: Zad z cechą podzielności przez 4 ja bym wykazała to tak: rozpatrując: ¹₄= 0,25 .... liczba zawierająca dwa ostatnie miejsca podzielna przez 4 bo 0,25:4= 0,0625 podobnie : podzielność przez 8 ¹₈= 0,125 ..... liczba zawierająca trzy ostatnie miejsca podzielna przez 8 bo 0,125:8=0,015625 tę ostatnią można wykazać podzielność przez 2 i następnie przez 4 bo 0,125:2= 0,0625 ....a ta już podzielna przez 4 bo 0,0625:4= 0, 015625 PS: AS .... mogę prosić o inną wersję dowodu

Miś: AS..... czym ta "majętność" się przedstawia?

AS: Podzielność przez 4 Każdą liczbę można przedstawić w postaci 100*A + ba np. 23456 = 234*100 + 56 Ponieważ 100 jest podzielne przez 4 więc wystarczy by końcówka ba była podzielna przez 4. Jeżeli końcówkę ba rozwiniemy do postaci 10*b + a = 8*b + 2*b + a to otrzymamy nową regułę. Ponieważ 8*b jest podzielna przez 4 wystarczy,że 2*b + a jest podzielne przez 4. np. liczba 37252 jest podzielna przez 4 bo końcówka 52 jest podzielna przez 4 lub 2*5 + 2 = 12 jest podzielna przez 4. Podzielność przez 8 Każdą liczbę można przedstawić w postaci 1000*A + cba np. 23456 = 23*1000 + 456 Ponieważ 1000 jest podzielne przez 8 więc wystarczy by końcówka cba była podzielna przez 8 Rozwińmy cba do postaci 100*c + 10*b + a = .96*c + 8*b + 4*c + 2*b + a = 8*(12*c + b) + 4*c + 2*b + a Ponieważ wyrażenie 8*(12*c + b) jest podzielne przez 8 wystarczy,że 4*c + 2*b + a jest podzielne przez 8 np. 467576 jest podzielne przez 8 bo 576/8 = 72 − liczba całkowita lub 4*5 + 2*7 + 6 = 40 która jest podzielna przez 8 a więc i cała pierwotna liczba jest podzielna przez 8.

AS: Oj Misiu! Nic z Twego wnioskowania nie rozumiem. Załączam wyrazy sympatii.

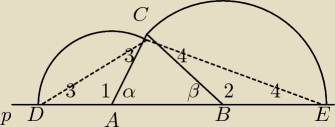
AS: Zbudować konstrukcyjnie trójkąt mając dane: αobwód trójkąta i jego dwa kąty wewnętrzne. Analiza: Niech ΔABC będzie tym trójkątem poszukiwanym. Odkładając na prostej p odcinki AD = AC i BE = BC otrzymamy odcinek DE będący danym obwodem trójkąta. Trójkąty ADC i BCE są trójkątami równoramiennymi. Wobec tego: ∠1 = 180 − α , ∠2 = 180 − β , ∠3 = α/2 , ∠4 = β/2 Konstrukcja: Na prostej p odkładam odcinek DE = obwodowi trójkąta. Przy punkcie D buduję kąt DAC = α/2 a przy punkcie E kąt BEC = β/2. Przecięcie tych ramion da mi punkt C − pierwszy znaleziony wierzchołek trójkąta. Przy odcinku CD ponownie wykreślam kąt DCA = α/2 a przy odcinku CE kąt BCE = β/2. Ramiona tych kątów wskażą następne wierzchołki trójkąta czyli punkty A i B

AS: Do Miś. Więcej w łepetynie.

Miś: Coś dla rozgrzewki umysłu ........ (łatwe) zad/ Podać liczby całkowite dodatnie "a" dla których: a³ +3 jest podzielne przez a+3 .

Miś: U mnie leje deszcz.... wrrr... dla poprawy samopoczucia wrzucam zadanko zad2/ Wykazać,że równanie: x*(x +1)*( x+2)= 2009³ nie ma pierwiastków całkowitych.

Paula: Pomoże ktoś mi, ? Jutro muszę oddać pracę z zadaniami na koniec semestru, a brakuje mi paru zadań 1. Odcinek drogi o długości 1800 metra wznosi się pod kątem 4 stopnie 36 '. Jaka jest różnica poziomów początku i końca tego odcinka drogi.

Miś: Już Ci podałam rozwiązanie

Serdeczna: o kurde, ludzie są WAKACJE !

Miś: A TY co tu robisz?

xpt: Serdeczna − dzięki, że zauważyłaś, że NIEKTÓRZY mają wakacje . . .

AS: Podać liczby całkowite dodatnie "a" dla których: a3 +3 jest podzielne przez a+3 . Przekształcam a³ + 3 = a³ + 27 − 24 = (a + 3)*(a² − 3*a + 9) − 24 Po podzieleniu przez a + 3 otrzymuję wyrażenie W = a² − 3*a + 9 − 24/(a + 3) By W było całkowite a + 3 musi być dzielnikiem 24. Dzielnikami 24 są liczby 1,2,3,4,6,8,12,24 Wobec tego mam szereg równań do rozwiązania a + 3 = 4 ⇒ a = 1 a + 3 = 6 ⇒ a = 3 a + 3 = 8 ⇒ a = 5 a + 3 = 12 ⇒ a = 9 a + 3 = 24 ⇒ a = 21

AS: Wykazać,że równanie: x*(x +1)*( x+2) = 2009³ nie ma pierwiastków całkowitych. Podstawiając do lewej strony równości za x dowolną liczbę całkowitą czynniki będą wyrazami pewnego ciągu arytmetycznego o różnicy 1. Prawa strona jest iloczynem trzech takich samych liczb pierwszych mających za dzielniki 1 i siebie samą. Każdy z czynników x , x + 1 , x + 2 musiałby przyjąć wartość 2009 żeby równość mogła zaistnieć, co nie jest możliwe.

Bogdan: Dzień dobry. W zadaniu "Podać liczby całkowite dodatnie a, dla których: a³ +3 jest podzielne przez a+3" zamiast prostego zresztą przekształcenia pokazanego przez Asa, można również wykonać

	24
zwykłe dzielenie: (a3 + 3} : (a + 3), w wyniku którego otrzymujemy a2 − 3a + 9 −
	a + 3

	24
i dalej analizując ułamek		postępujemy tak samo jak As.
	a + 3

Pytanie do Asa w sprawie zadania "Wykazać,że równanie: x*(x +1)*( x+2) = 2009³ nie ma pierwiastków całkowitych", napisałeś (a może napisałaś?): "Prawa strona jest iloczynem trzech takich samych liczb pierwszych" − jakie liczby pierwsze masz na myśli?, bo 2009 = 41*7². Lewa strona równania, czyli x*(x +1)*( x+2) jest dla x całkowitych liczbą parzystą i podzielną przez 3 bo jest iloczynem trzech kolejnych liczb całkowitych, prawa strona, czyli 2009³ = 41³*7⁶ jest liczbą nieparzystą i dodatkowo niepodzielną przez 3, a więc lewa strona nie równa się prawej stronie.

Bogdan: Witam Misiu i Timie . Tim − mamy jedną sprawę do wyjaśnienia. Napisałeś wyżej: wielokrotność 10 czyli 10^k, czy dalej tak uważasz? A jak zapiszesz np. wielokrotność liczby 4, czy 4^k ?

Miś:

♊: Tim − bogdan ma na myśli to, że 20 też jest wielokrotnością 10, a nie ma k należącego do liczb naturalnych, dla których 10^k = 20

AS: Mea culpa! Nie miałem pod ręką tablicy liczb pierwszych o takim zasięgu i przyjąłem że jest dokładnie pierwsza tj. ma tylko dzielnik 1 i 2009. Gdybym znał ten rozkład to podałbym właściwe uzasadnienie. Sorry!

Eta: Ok Wystarczyło podać w uzasadnienieniu ,że iloczyn x(x+1)(x +2) jest iloczynem trzech kolejnych liczb całkowitych tak jak : wyjaśnił to Bogdan. Pozdrawiam

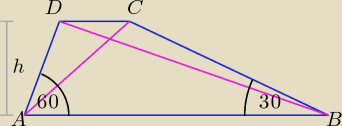
Bogdan: Kiedyś na forum pojawiło się następujące zadanie. W trapezie ABCD przyjmujemy oznaczenia: a = |AB|, b = |CD|, c = |BC|, d = |AD|, e = |BD|, f = |AC|, h − wysokość trapezu. Dane są: α = |<BAD| = 60^o, β = |ABC| = 30^o, e² − f² = 20 (zamiast liczby 20 można wstawić dowolną liczbę lub oznaczenie literowe, ta liczba jest dana). Obliczyć pole powierzchni trapezu. To zadanie zostało wtedy rozwiązane. Znalazłem inny i dość zadziwiający sposób rozwiązania tego zadania, ale nim go przedstawię, proszę spróbować najpierw je rozwiązać i pokazać rozwiązanie.

AS: Proponuję nowe zadanie do rozwiązania Dane są: cosα + cosβ = a sinα + sinβ = b Znaleźć: sin(α + β) i cos(α + β)

Bogdan: Pamiętacie, jak przed maturą do znudzenia wrzucałem tutaj zadania dla maturzystów z liczbą 2009? Jest taka moda na umieszczanie w zestawach egzaminacyjnych zadań zawierających liczbę aktualnego roku, chciałem uczulić maturzystów na rozkład tej liczby. Pozdrawiam wszystkich wiernych temu forum .

Bogdan: Proponuję, abyśmy wymyślali i umieszczali tutaj zadania z liczbą 2010, będzie za rok jak znalazł.

tim: Bogdan oraz | | Zakręciłem się wmawiałem sobie, że wielokrotności 10 to 10,100,1000.. i jakoś dziwnie wyszło.. ale dobra, teraz już wiem. Wracając do zadania − czy to można tak napisać? x(x+1)(x+2) = 2009³ Gdyby istniały całkowite to: parzysta * parzysta = parzysta nieparzysta * nieparzysta = nieparzysta parzysta * nieparzysta = parzysta Więc w ciągu x(x+1)(x+2) 1) x, x+2 są parzyste, więc wynik jest nieparzysty, natomiast 2009 * 2009 * 2009 jest nieparzysta również 2) x + 1 jest parzysta, więc wynik jest parzysty, co mija się z prawdą (⁾ I dalej mamy jeden wariant: x, x+1, x+2 gdzie x, x+2 są parzyste, a że jeden musi być równy 2009 (patrz AS) więc sprawdzamy: L = 2008 * 2009 * 2010 P = 2009 * 2009 * 2009 L = x(x+1)(x+2) = (x² + x)(x + 2) = x³ + 3x² + 2x, gdzie x = 2008 P = (x − 1)³ = x³ + 3x² − 3x + 1 Gdyby L = P, to 2x = −3x + 1, co jest sprzeczne. Odp. Nie ma.

tim: A wieloktoność to k * 10

sylwia gdańsk: matura 2010XD jestem nastepna<strach>

tim: Zresztą teraz patrzę, czy nie wystarczyło by rozwinąć wzory skróconego mnożenia (czyli samo od słowa sprawdzamy)

tim: Zapraszam na IRCa (|| podaj link )

Bogdan: Sylwio, już masz tremę?

tim: Taaa.. Wpadka: Jeszcze raz: L = x(x+1)(x+2) = (x² + x)(x + 2) = x³ + 3x² + 2x P = (x + 1)³ = x³ + 3x² + 3x + 1 L = P ⇔ 2x = 3x + 1 → 5x = −1, więc x nie należy do całkowitych. Teraz lepiej chyba

Bogdan: No, nieźle Tim.

tim: Rozumiem, że rozwiązanie uznane?

sylwia gdańsk: Bogdan nie!

sylwia gdańsk: nie z matmy

Bogdan: Sylwio, ale dlaczego? Przecież przy systematycznym rozwiązywaniu zadań i aktywności na tym forum matma staje się najłatwiejszym przedmiotem maturalnym

Bogdan: Tim

sylwia gdańsk: Bogdan no ale nie mówie o matmie

sylwia gdańsk: chociaż roz z matmy pewnie trudne

tim: Chyba pierwszy raz dostaje od ciebie brawo.. ... to dla mnie zaszczyt

sylwia gdańsk: tim dali Ci 6 chyba nie?

sylwia gdańsk: z matmy

tim: Ale w szkole? 6,00 to logiczne xD

Bogdan: A gdzie tam, Sylwio trudne, może tylko trochę ciekawsze. Wyobraź sobie swoją satysfakcję i podziw innych za dobre zaliczenie matury rozszerzonej z matmy. Czy nie warto o to powalczyć? Dzisiaj niektóre uczelnie techniczne w Polsce przyznają miesięczne stypendium w kwocie 1000 zł za podjęcie u nich studiów, warunkiem jest znajomość szkolnej matematyki.

sylwia gdańsk: heheheh no wlasnie Bogdan slyszlam ze roz z matmy to kosmos w porownaniu do podstawy

sylwia gdańsk: Bogdan a o uczelni technicznej toraczej nie mysle

Eta: Timuś dorzucam

Bogdan: O kosmosie to plotki Sylwio leni, którym nie chce się nauczyć nawet tabliczki mnożenia.

sylwia gdańsk: tim a gdzie

sylwia gdańsk: ja tam matme lubei ale zeby sie na roz pchac to raczej nie

sylwia gdańsk: Bogdan a co myslisz ze roz jest na niskim poziomie?

Bogdan: Niski poziom lub wysoki poziom, to względne pojęcia. Myślę, że uczeń osiągający oceny co najmniej dobre, może spokojnie myśleć o maturze rozszerzonej. Uczeń z niższymi ocenami maturę rozszerzoną uzna, że jest na wysokim poziomie. Trzy lata temu (a może dwa?) zakres materiału został poważnie okrojony i teraz matura jest, jak sądzę łatwiejsza. Bez względu na to, jaką decyzję podejmiesz, życzę Ci powodzenia i zachęcam do rozwiązywania (codziennie) zadań. Praktyka, jak to mówią, czyni mistrza.

sylwia gdańsk: hehehe dzieki

sylwia gdańsk: tylko ze za bardzo nei ma zadan

sylwia gdańsk: a ktos moze powiedziec o materiale cos w 3 klasie bo chyba tak samo mniej wiecej jest w LO

sylwia gdańsk: szczerze to najbardziej okrojonym przedmiotem jest fizyka heh u mnie podstawa to byly 2 ksiazki po 30 stron i koniec

sylwia gdańsk: sory 79 stron sprawdzilam wydawala mi sie mniejsza jakas

sylwia gdańsk: ale glownie tam nic nie ma rysunki i jakies zadania powtorzeniowe heh

kamerling: U mnie dopiero za 2 latka matura... myślisz Bogdan, że rozwiązywanie codziennie samodzielnie zadań pomoże i np. za rok będzie już mi się 'łatwiej myślało' ? Czy można to uznać za trening? Co o tym sądzisz?

Bogdan: Zdecydowanie kamerling pomoże. Nie można robić sobie zbyt długich przerw, w czasie wakacji również trzeba rozwiązywać zadania. I bardzo ważna zasada − nie można odpuścić żadnemu zadaniu, które nie chce się nam na początku poddać. Tak długo trzeba podchodzić do takiego zadania, aż go rozwiążemy. Tim dostał dzisiaj ode mnie brawa właśnie za nieustępliwość i upartość w dążeniu do rozwiązania. Przy okazji szukamy nowych narzędzi (metod, wzorów, twierdzeń itp) gdzie tylko się da. Teraz jest łatwiej, internet to kopalnia wiedzy i niewyczerpane oraz łatwo dostępne źródło informacji. Jakże często słyszymy od uczniów − nie wiem, nie umiem, nie rozumiem, pomocy, ratunku, itp. zaraz po przeczytaniu treści zadania bez próby wgryzienia się w to zadanie. Trzeba wierzyć w siłę swojego rozumu. Podsumowując − najlepszym sposobem na matematykę jest rozwiązywanie zadań, "w piątki, świątki i w niedziele". Trening w każdej dziedzinie daje efekty. Pozdrawiam

kamerling: Bardzo dziękuje Bogdan za odpowiedź. Pozdrawiam

pinio: Bogdan i Eta super ,kiedy Ja taki będę.Ćwiczę możę się uda.

Eta: Ćwicz pinio ... jak podpowiada Bogdan: " świątki, piątki i niedziele" ! Efekty zauważysz bardzo szybko Pozdrawiam!

tim: Jestem PS. Ładna metoda? (podniecony ) PS2. Sylwiu, ale ze co? :

Bogdan: Elegancka Timie

Eta:

Eta: Zad... dla Timusia Wykaż ,że a= √6 − 2√5 − √5 jest liczbą całkowitą .

Adam: Hej.Mam prośbe o rozwiązanie zadań które potrzebne mi są na jutro do szkoły.NIe daje ra dy ich rozwiązac z powodu mojej dyskalkuli. Będe wdzieczny za kazda pomoc. 1,Jaką długość ma promień okręgu wpisanego w romb o przekątnych długości 10cm i 12cm. 2,Oblicz długość promieni okręgów wpisanych i opisanych dla trójkąta prostokątnego o bokach długości 8,15 i 17. 3,Oblicz pole kola wpisanego w trojkąt równoboczny o boku 4cm. 4,Odcinek A'B' jest podobny do odcinka AB w skali 5.Jaką dlugość ma odcinek A'B' jeśli odcinek AB ma długość 2? 5,Kąt α' jest podobny do kąta α w skali 3.Kąt α ma miarę 30st.Jaką miare ma kąt α? 6,Trójkąt K'L'M' jest podobny do trójkąta KLM w skali ¹₃ jaki obwód ma trójkąt KLM,jeśli obwód trójkąta K'L'M' jest równy 60?

Eta: zad1/ r= ¹₂h należy obliczyć h P= ¹₂*e*f gdzie e, f −−− długości przekątnych rombu P= ¹₂*12*10 = 60 [j²] przekątne dzielą romb na cztery przystające trójkąty prostokątne zatem z tw. Pitagorasa obliczamy długość "a" boku rombu: a² = (¹₂e)² + ( ¹₂f)² a² = 36 + 25 => a² = 61 => a= √61 zatem: P= a*h => √61*h= 60

	60
to: h=
	√61

	30
więc r=
	√61

	30√61
więc : r =
	61

zad2/ a= 8 b= 15 c= 17

	c		17
Rop =		...... to R=
	2		2

R= 8,5 [ j]

	P
rwp=
	p

gdzie P−−− pole trójkąta p −− połowa obwodu zatem:

	a+b+c
P= 12a*b p=
	2

P= ¹₂*8*15 = 60 [j²]

	40
p=		to p= 20 [j]
	2

zatem r_wp= ⁶⁰₂₀ r_wp= 3 [j] zad3/ r_wp= ¹₃*h_Δ

	a√3
hΔ=
	2

	4√3
to hΔ=		= 2√3
	2

więc: r_wp= ^2√3₃ [j] zad4/ A^'B^' ~ AB w skali k= 5 to: I A^'B^'I = k*IABI IA^'B^'I= 5*2 IA^'B^'I= 10 zad 5/ podobnie: α^' ~ α w skali k= 3 to α^'= k*α α^'= 3*30^o α^' = 90^o zad6/ Δ K^'L^'M^' ~ Δ KLM w skali k = ¹₃

	ObΔ K'L'M'
to		= k
	ObΔKLM

	60		1
to:		=
	ObΔKLM		3

więc: Ob ΔKLM = 60 * 3 = 180 [j]

tim: Hm... Eto... Zagadka dla mnie... ale dosyć trudna (dla mnie )... muszę się trochę pogłowić

tim: No i już Najpierw liczyłem: √6 − 2√5 − √5 = a ² 6 − 2√5 − 2√30 − 10√5 + 5 = a² I nawet do 4 141 + 120 − 40√5 − 44√5 + 8√150 − 50√5 − 44√30 − 10√5 = a⁴ A nie spostrzegłem wzoru skróconego mnożenia, gdyż 6 − 2√5 = 1 − 2√5 + 5 = (1 − √5)² I mamy: √(1 − √5)² − √5 = a |1 − √5| − √5 = a √5 − 1 − √5 = a a = − 1 a jest całkowite

tim: Ach .. ty Eta Teraz ja mam zadanko:

	a		b		c
Udowodnij, że jeżeli:		+		+		= 1 to:
	b + c		c + a		a + b

a2		b2		c
	+		+		= 0
b + c		c + a		a + b

tim: Tam miało być c² −−> poprawka:

a2		b2		c2
	+		+		= 0
b + c		c + a		a + b

Adam: O matko jesteście wielcy Dzieki Wielkie nie spodziewalem sie tak szybkiej i konkretnej odpowiedzi Dziękuje

Adam: P.S. Oczywiscie Dzięki dla Ciebie Eta

Adam: Głupio mi prosić..Ale dostalem kolejne 12 zadan znów na jutro.Bo potrzebuje dużo ocen.Chcialoby sie wam Sama geometria

Michał KAS: Zad. Rozwiąż równanie a) |−|x|+2|=4 b) |−|x−1|+4|=7 Zad. Oblicz

4128*216−5*832:49*1647
5*[25*(324)3]4*5,9

magda: siema

magda: ktos to robi te zdania michala

Adam: 1,Jaka jest wysokość walca,którego średnica podstawy jest równa 12cm,a objętość jest równa 72π. 2.Koło wielkie kuli ma obwód 16π.Oblicz objętość kuli. 3.Pierścien kołowy o promieniach R=5cm i r=3cm obrócono wokół średnicy.Oblicz objętość powstalej bryły 4,Oblicz przekątną graniastosłupa prawidłowego czworokątnego o krawędzi podstawy 4 i krawędzi bocznej 5. 5.Jaką długość ma krawędź ośmiościany foremnego o krawędzi 3? 6,Oblicz wysokość czworościany foremnego o krawędzi 4, 7.Oblicz pole powierzchni całkowitej i objętość a)graniastosłupa prawidłowego trojkątnego i krawędzi podstawy 4cm i krawędzi bocznej 6cm. b)ostrosłupa prawiodłowego o krawędzi podstawy równej 4cm i wysokości równej 1cm. c)graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy 3cm i krawędzi bocznej 5cm. 8.Ile materiału potrzea na uszycie namiotu w kształcie walca o średnicy podstawy 3m i wysokości 1m,na którym umieszczono półkulistą kopułę? 9.jaką bryłę obrotową otrzymano przez obrót rombu: a)wokół jego przekątnej b)wokół jego boku? 10.Przekątna ściany bocznej sześciany ma długość 2√6.Oblicz objętość tego sześcianu. NAprawde uratowalibyscie mnie przed niezdaniem. ... Proszę

Adam: 1,Jaka jest wysokość walca,którego średnica podstawy jest równa 12cm,a objętość jest równa 72π. 2.Koło wielkie kuli ma obwód 16π.Oblicz objętość kuli. 3.Pierścien kołowy o promieniach R=5cm i r=3cm obrócono wokół średnicy.Oblicz objętość powstalej bryły 4,Oblicz przekątną graniastosłupa prawidłowego czworokątnego o krawędzi podstawy 4 i krawędzi bocznej 5. 5.Jaką długość ma krawędź ośmiościany foremnego o krawędzi 3? 6,Oblicz wysokość czworościany foremnego o krawędzi 4, 7.Oblicz pole powierzchni całkowitej i objętość a)graniastosłupa prawidłowego trojkątnego i krawędzi podstawy 4cm i krawędzi bocznej 6cm. b)ostrosłupa prawiodłowego o krawędzi podstawy równej 4cm i wysokości równej 1cm. c)graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy 3cm i krawędzi bocznej 5cm. 8.Ile materiału potrzea na uszycie namiotu w kształcie walca o średnicy podstawy 3m i wysokości 1m,na którym umieszczono półkulistą kopułę? 9.jaką bryłę obrotową otrzymano przez obrót rombu: a)wokół jego przekątnej b)wokół jego boku? 10.Przekątna ściany bocznej sześciany ma długość 2√6.Oblicz objętość tego sześcianu. NAprawde uratowalibyscie mnie przed niezdaniem. ... Proszę

AS: a) |−|x| + 2| = 4 Przypominam: |x| = x dla x ≥ 0 −x dla x < 0 −|x) + 2 = 4 lub −|x| + 2 = −4 −|x| = 4 − 2 −|x| = −4 − 2 −|x| = 2 −|x| = −6 |x| = −2 odpada |x| = 6 ⇔ x = −6 lub x = 6 (Odp.) bo wartość bezwzględna jest zawsze ≥ 0 b) |−|x − 1| + 4| = 7 −|x − 1| + 4 = 7 lub −|x − 1| + 4 = −7 −|x − 1| = 7 − 4 −|x − 1| = −7 − 4 |x − 1| = −3 odpada |x − 1| = 11 x − 1 = 11 lub x − 1 = −11 x = 12 lub x = −10 (Odp)

tim: Heh ... As a ja rozwiązuję to w drugim poścvie

tim: Zadania ADAMA:

tim: 1: d = 12cm V = 72π r = 6cm V_walca = πr²H 72π = π * 6² * H 72 = 36H H = 2

tim: 2: 2πR = 16π R = 8

	4
Vkuli =		πR3
	3

	4
V =		* π * 83
	3

	4
V =		* 512π
	3

V = 682²₃π

AS: Ależ rywalizacja! Z dopingiem.

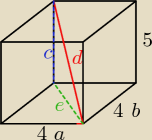tim: 3... Zostawiam dla kogoś 4: Rysunek: graniastosłup prawidłowy czworokątny = graniastosłup o podstawie kwadratu. METODA A: Widzimy, że przekątna graniastosłupa, przekątna podstawy oraz krawędź boczna tworzą trójkąt prostokątny, zatem: c² + e² = d² Musimy znaleźć długość e: a² + b² = e² 4² + 4² = e² e = 4√2 Mamy c i e. Podstawiamy do wzoru: 5² + (4√2)² = d² 25 + 32 = d² d = √57 METODA B: Korzystamy z wzoru na długość przekątnej w graniastosłupie: d = √a² + b² + c² d = √16 + 16 + 25 = √57

tim: Heh

magda: im moge wiedziec gdzie sie wybierasz jak skonczysz LO?

magda: tim mialo byc nie im heheh

magda: i jak CI idzie fizyka?

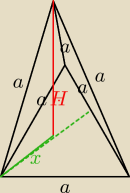tim: 5. Na pewno tak? O.o Jaką długość ma krawędź ośmiościanu o krawędzi 3? Odp. 3 6. Rysunek: Czworościan foremny = Cztery ściany w kształcie trójkątów równobocznych. METODA A:

	2
Korzystając z własności trójkąta równobocznego mamy odcinek x =		h (h = wysokość podstawy
	3

	√3		2		√3		√3
=		a), więc x =		*		a =		a
	2		3		2		3

Z tw. Pitagorasa wynika: x² + H² = a²

	√3
(		a)2 + H2 = a2
	3

3
	a2 + H2 = a2
9

	2
H2 =		a2
	3

H = √²₃a <<−−−− H = √²₃ * 4 METODA B. Korzystamy z wzoru na wysokość czworościanu foremnego (dostępnego np. w książce) (który wyprowadziłem wcześniej) H = √²₃a H = √²₃ * 4

tim: madziu... Chciałaś powiedzieć jak skończe GIM ? Idę chyba do 3 LO w Gdańsku, bądź do 3 LO w Gdyni.

magda: ale ja pytam po lo

tim: A ja wiem? To dopiero za raz.., dwa.., trzy.. cztery.. pięć... lat

magda: no ja ale nei zastanawiales sie na prawde?

tim: Nie... A czemu pytasz?

magda: a tak sobie

tim: Mów Czemu xD A tak wgl to mnie znasz? xD

magda: skad? heheh nie znam

tim: A z forum?

Miś: Do Adam zad3/ powstała z obrotu bryła jest kulą o promieniu R= 5 z wydrążoną małą kulą ( współśrodkową ) o promieniu r= 3 zatem V_bryły = ⁴₃πR³ − ⁴₃πr³ Vbr.= ⁴₃π( 5³ − 3³) = ⁴₃π*98 [j³] zad8/ P_c = ¹₂P_kuli + P_bwalca P_c= 2πr² +2πrh gdzie r= ³₂ h= 1 P_c= 2π*⁹₄ + 2π*³₂ P_c= ⁹₂π + 3π P_c= ¹⁵₂*π P_c= 7,5*3,14 =23, 55m²

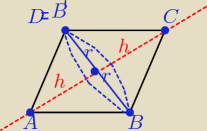
Miś: zad9/ IACI = f IDBI= e w wyniku obrotu rombu dookoła przekątnej powstaje bryła złożona z dwóch sklejonych podstawami przystających stożków o wymiarach: 1/ jezeli obrót jest wokół przekątnej "f" to: r= ¹₂e h= ¹₂f 2/ " " " " " "e" to: r= ¹₂f h= ¹₂e

♊: tim prosił o link do kanału IRC (kanał tymczasowy i nieoficjalny ) jeden z linków: http://widget.mibbit.com/?server=irc.quakenet.org&nick=gosc_%3F%3F%3F&channel=%23matematyka.pisz.pl&customprompt=Witamy na nieoficjalnym kanale IRC serwisu matematyka.pisz.pl&customloading=maybe you need to close other Mibbit windows first...&settings=22041f31cac0adf2d1959cdc21aed853 Podobna odsłona http://widget.mibbit.com/?server=irc.quakenet.org&nick=gosc_%3F%3F%3F&channel=%23matematyka.pisz.pl&settings=22041f31cac0adf2d1959cdc21aed853 można też na http://webchat.quakenet.org ale trzeba wpisać nazwę kanału #matematyka.pisz.pl i swój nick (w 2ch pierwszych linkach nick jest gosc_xxx gdzie x to losowa cyfra )

♊: pierwszy link nie działa − wybaczcie

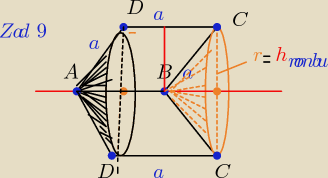
Miś: Dla Adam bryłą powstałą z obrotu rombu wokół boku jest: walec z wydrążonym stożkiem oraz nałożonym stożkiem( o tych samych wymiarach) których podstawą jest koło o promieniu r = h_rombu V_bryły = V_walca DCD^'C^'

magda: x ¹⁰ : (x²+x−2) podzien wielomian zerknie ktos jak to rozw?

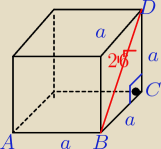
Miś: Zad 10/ trójkąt BCD jest prostokątny i równoramienny: zatem IBDI² = a² +a² 2a² = (2√6)² 2a² = 4*6 a² = 12 a= √12 = 2√3 a= 2√3 V= a³ => V= ( 2√3)³ = 8*3√3 = 24√3 [ j³]

Vax: Zaczynają się wakacje, więc postanowiłem odświeżyć temat Na początek może zarzucę zadankiem: Uzasadnij, że liczby a(1−b) , b(1−c) , c(1−a) nie mogą być wszystkie jednocześnie większe od

	1
		(a,b,c rzeczywiste )
	4

Pozdrawiam.

eN'Roses: Zad 2 Bogdana mozna bylo by zrobic tak ze podzielic obu stronnie przez n! a potem wyliczyc granice? podobnie jak zrobil to AS?

Vax: Tak, doprowadzamy to do postaci:

	1
n > (1+		)n
	n

Teraz zauważamy, że z założenia mamy n ≥ 3, ale prawa strona dąży do e < 3, skąd wynika teza,

	1
co do mojego zadania to daję podpowiedź, że na początku można dowieść, iż x(1−x) ≤		dla
	4

dowolnej liczby rzeczywistej Pozdrawiam.

Godzio: A taki układ : a = 2 c = − 1

	1
b =		?
	2

	1
a(1 − b) = 2 * (1 −		) = 1
	2

	1
b(1 − c) =		(1 − (−1)) = 1
	2

c(1 − a) = − 1 * (1 − 2) = 1

	1
Wszystkie są >
	4

Vax: Eh, sorry za małe zamieszanie, nie dopisałem, że a,b,c ∊ (0;1) teraz jest ok.

Adrian: zadanie wydaje się trochę trudniejsze i nie wiem jak się za nie zabrać a mianowicie z jakiego wzoru na pochodne skorzystać. Wyznaczyć pochodne cząstkowe funkcji: f(x,y)=cos(x)√y−2x5y7 proszę o pomoc

Adrian: ∫xcos(2x)dx proszę o pomoc w rozwiązaniu tej całki

Jack: w innym poście rozwiązane...

Vax: Zauważyłem jeszcze jedno nierozwiązane zadanie z 21 czerwca (tim'a) wykaż, że jeżeli

a

b

c

a2

b2

c2

+

+

= 1 to

+

+

=0, mnożąc założenie

b+c

a+c

a+b

b+c

a+c

a+b

przez a otrzymujemy:

a2		ab		ac
	+		+		= a
b+c		a+c		a+b

Analogicznie przez b,c:

ab		b2		bc
	+		+		= b
b+c		a+c		a+b

ac		bc		c2
	+		+		= c
b+c		a+c		a+b

Sumujemy stronami:

a2		b2		c2		ab+ac		ab+bc		ac+bc
	+		+		+		+		+		= a+b+c
b+c		a+c		a+b		b+c		a+c		a+b

a2		b2		c2		a(b+c)		b(a+c)		c(a+b)
	+		+		+		+		+		= a+b+c
b+c		a+c		a+b		b+c		a+c		a+b

a2		b2		c2
	+		+		+a+b+c = a+b+c
b+c		a+c		a+b

a2		b2		c2
	+		+		= 0 cnd
b+c		a+c		a+b

Pozdrawiam.