Wyprowadź wzór na pole powierzchni figury płaskiej... zenek135: Witam Mam problem z prostym − na pierwszy rzut oka − zadankiem. Zadanie składa się z dwóch części. 1) Wyprowadź wzór na przedstawione niżej − zakreskowane pole powierzchni, używając symboli: D − średnica zewnętrzna (lub R − większy promień) d − średnica wewnętrzna (lub r − mniejszy promień) p − wielkość przerwy P − pole powierzchni Tu znajduje się rysunek pola: http://img10.imageshack.us/img10/6897/pole3.png Właściwy problem pojawia się w części drugiej: 2) Używając wyprowadzonego wcześniej wzoru, sprawdź dla jakich wartości D spełniona jest nierówność: F / P < k Byłbym wdzięczny za pomoc.

imię lub nick.: ↑ ciekawe zadanie. przyznacie...

zenek135: Dla mnie to zadanie okazało się za ciekawe. Jest to część większego projektu z podstaw konstrukcji maszyn. Jeśli nie uda mi się tego rozwikłać to projekt najprawdopodobniej nie zostanie skończony. Bardzo dużo czasu i wysiłku włożyłem już w ten projekt, więc bardzo mi zależy na rozwiązaniu.

Jakub: Piszesz "Właściwy problem pojawia się w części drugiej" tzn. masz już ten wzór na pole powierzchni czy nie? Jeśli chodzi o 2) to co oznaczają litery F i k. Z twojego postu to nie wynika, a z konstrukcji maszyn to raczej wielu specjalistów tu nie ma. Zadanie faktycznie ciekawe.

AS: Przysyłam wstępne rozwiązanie − prawdopodobnie ulegnie ono zmianie. Nie sprawdziłem do końca. s = p/obwód zewnętrzny = p/(2*π*R) − jest to część obwodu zewn. jaki przypadnie na przerwę. Taka sama część przypadnie na kąt środkowy odpowiadający szparze α = s*(2*π) = p/R kąt wyrażony w radianach Pole pierścienia pełnego P1 = π*(R² − r²) Pole jednej szpary P2 = 1/2*R²*α − 1/2*r²*α = 1/2*α*(R² − r²) = 1/2*p/R*(R² −r²) Szukane Pole S = P1 − 2*P2 = π*(R² − r²) − 2*1/2*p/R*(R² − r²) S = (R² − r²)*(π − p/R) Tak na słowo honoru, na razie nie mam pełnej pewności co do poprawności. W każdym razie na razie błędu nie dostrzegam. W drugiej części co oznacza F i k?

zenek135: Celowo sformułowałem zadanie tak aby matematycy nie znający się na konstrukcji maszyn nie musieli się nimi zajmować, dlatego nie wspominałem o zbędnych szczegółach. Tak więc: F − działająca siła (ściskająca detal o podanym przekroju) k − parametr określający wytrzymałość stali na ściskanie Traktujcie je jako wielkości dane, przemieszczając je w równaniu wedle potrzeby. Nie mogę podać konkretnych wartości ponieważ nie są to stałe (będę musiał zmieniać te parametry wedle potrzeby)

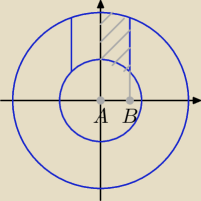
Bogdan: A = (0, 0), B = (^P₂, 0) Równanie okręgu o promieniu R: x² + y² = R² ⇒ y = √R² − x² dla x ∊ <0, R>, Równanie okręgu o promieniu r: x² + y² = r² ⇒ y = √r² − x² dla x ∊ <0, r> Zastosujemy rachunek całkowy. P/2 Pole części zakreskowanej: P = ∫ (√R² − x² − √r² − x² ) dx 0 Uwaga: ∫ √a² − x² dx = ¹₂arcsin ^x_|a| + ¹₂x√a² − x² + C

Bogdan: Coś niewyraźnie wyszły ułamki i jest nieścisłość w ostatnim zapisie.. Poprawiam:

	P
B = (		, 0)
	2

	1		x		x
∫ √a2 − x2 dx =		a2 arcsin		+		√a2 − x2 + C
	2		|a|		2

Leszek: Bogdanie a jeżeli mamy pole wycinka koła πR²*α to da się zamienić ten wzór na wzór z funkcją trygonometryczną na z sinusem kąta α

Bogdan: Leszku, pole wycinka koła przy zastosowaniu miary stopniowej kąta wyraża się wzorem:

	α		1
Pw =		πR2, a przy zastosowaniu miary łukowej: Pw =		αR2. O który
	360		2

z tych wzorów pytasz? Domyślam się , że o drugi, ale potwierdź. α − miara kąta środkowego

Leszek: tak o ten drugi myślałem czy nie ma wzoru z zastosowaniem funkcji trygonometrycznych, ale jak widze nie ma, dzięki za pomoc

AS: Wzór poprawnie wyliczony. Z punktem 2) proszę sobie samemu radzić. Nie bardzo wiem co z tym fantem począć − a nie chcę wprowadzać w błąd.

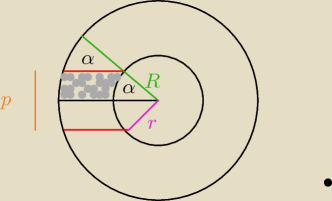
Mariusz: rRp do ASA czy nie jest tak może Asie ta, że pole części szarej jest równe

1		1		1		1
	αR2−		αr2−		α(R−r)2 =		α(2Rr−2r2)=α*r*(R−r)
2		2		2		2

Pytam tak z ciekawości, bo nie bardzo rozumiem dlaczego dałeś

1
	α(R2−r2)
2

AS: Do Mariusza. Masz zupełną rację − ja dobrze nie przypatrzyłem się rysunkowi i przyjąłem ścianki skośnie ustawione zgodnie z promieniami. Twoje wyliczenie jest poprawne. Szukane pole będzie miało postać S = π(R² − r²) − 2*r*p*(R − r)/R Jak to dobrze że są cenzorzy.

AS: Oczywiście,że chochlik znów urzęduje Szukane pole będzie miało postać S = π*(R² − r²) − 4*r*p*(R − r)/R

Mariusz: Do ASA a mógłbyś mi jeszcze powiedzieć dlaczego α=p/R

zenek135: Trochę się pogubiłem Wiem że π*(R² − r²) to jest pole pierścienia, jeżeli tak to 4*r*p(R − r)/R to jest pole tej przerwy tylko nie wiem jak ta przerwa jest policzona, więc prosił bym jeszcze o wytłumaczenie. Jeżeli to jest dobrze policzone to teraz trzeba podstawić ten wzór do nierówności w punkcie drugim:

F
	<k
4*r*p*(R − r)   π*(R2 − r2) −   R

po uwolnieniu od niewymierności i przeniesieniu wszystkiego na lewą stronę mamy:

	4*r2*p		F
π*R2−π*r2−4*r*p+		−		>0
	R		k

Następnie mnożę obie strony przez R aby pozbyć się go z mianownika i mam:

	F
π*R3−(π*r2+4*r*p+		)*R+4*r2*p>0
	k

wyznaczając dla jakich wartości R prawdziwa jest nierówność stopnia trzeciego rozwiążemy punkt 2) Z tym też sobie raczej nie poradze Jeszcze jeśli chodzi o pole... ja też na coś wpadłem. Za chwilę napiszę co wymóżdżyłem.

AS: Przyjąłem że p to jest łuk odpowiadający szparze. p/(2*π*R) określa jaka część zewnętrznego okręgu przypada na łuk. Taka sama część przypadnie na kąt środkowy α = p/(2*π*R)*2*π = p/R

Mariusz: chyba ten wzór końcowy nie jest do końca dobrze wyprowadzony , musze pomyśleć

zenek135: Więc tak: korzystam ze wzoru na odcinek koła

	1
S =		*r2(α−sinα)
	2

wprowadzam brakujące oznaczenia: http://img41.imageshack.us/img41/7162/pole4.png zastępuje brakujące oznaczenia

0,5*p		1		p
	= sin(		*β) ⇒ β = 2*arcsin(		)
R		2		2*R

0,5*p		1		p
	= sin(		*α) ⇒ α = 2*arcsin(		)
r		2		2*r

Podwojona różnica pola większego i mniejszego odcinka koła:

	1		p		p
S = 2*(SR − Sr)=2*(		*R2*(2*arcsin(		)−sin(2*arcsin(		)))−
	2		2*R		2*R

	1		p		p
−		*r2*(2*arcsin(		)−sin(2*arcsin(		)))
	2		2*r		2*r

A teraz pozostaje taki sam problem jak poprzednio:

F		p		p
	<(R2*(2*arcsin(		)−sin(2*arcsin(		)))−r2*(2*arcsi
k		2*R		2*R

	p		p
n(		)−sin(2*arcsin(		)))
	2*r		2*r

Również nie wiem jak sprawdzić dla jakich wartości R prawdziwa jest nierówność

zenek135: Ale p to nie może być łuk odpowiadający szparze, bo przy większych wielkościach p różnica między długością cięciwy a łukiem będzie spora...

Mariusz: mi tez sie tak wydaje. Musze wykombinowac jak się pozbyć α z tego mojego wzoru

Bogdan: Powiedzcie proszę, w jakim programie sporządzacie takie zgrabne rysunki z oznaczeniami.

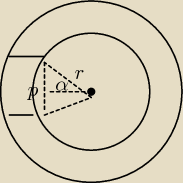
AS: To pozostaje tylko: sin(α) = (p/2)/r = p/(2*r) [1] Pole odcinka (wewnętrznego) Pow = 1/2*r²*(2*α) − 1/2*r²*sin(2*α) = r²*α − 1/2*r²*2*sin(α)*cos(α) Pow = r²*α − r²*sin(α)*cos(α) [2] Wyliczam cos(α) z wzoru jedynkowego cos(α) = √1 − p²/(4*r²) = 1/(2*r)*√4*r² − p² [3] [3] i [1] wstawiam do [2] Pow = r²*α − r²*p/(2*r)*1/(2*r)*√4*r² − p² Pow = r²*α − p/4*√4*r² − p² Analogicznie postąpić z odcinkiem zewnętrznym sin(β) = p/(2*R) Poz = R²*β − p/4*√4*R² − p² Kąty α i β odczytać z tablic bądź skorzystać z przybliżenia (dla niewielkich kątów) sin(x) = x − x³/6

zenek135: Ja swoje rysunki robię w programie AutoCAD.

zenek135: Kąt α może sięgać nawet 45^o (90⁰ wg moich oznaczeń) czy takie kąty można jeszcze uznać jako niewielkie?

zenek135: Kontynuując myśl rozpoczętą przez Bogdana: p/2

	1		p
∫√R2−x2dx =		*p*√R2−14*p2 + R2*arcsin(		)
	4		2*R

0 Więc pole:

	π		p
S=		(D2−d2)−p√R2−14p2+R2arcsin(		)+
	4		2R

	p
+p√r2−14p2+r2arcsin(		)
	2r

Zostaje jeszcze podstawić do punktu 2) Pole S potraktuję jako funkcję S(R)

	F		F
2)		<k ⇒ S(R)−		>0
	S(R)		k

	p
Tu również pojawia się ten koszmarny arcsin(		)
	2R

Powiedzcie mi czy można rozstrzygnąć dla jakich wartości R funkcja jest dodatnia np badając przebieg zmienności funkcji?