obliczenie ekstremum lokalnego
neocortex: Cześć, mam ciekawe wyzwanie z zadaniem, w którym należy obliczyć ekstremum globalne funkcji:
f(x)=x+
√x x należy[0,4]
Obliczenia:
po krótkich obliczeniach wychodzi mi:
x=
12√x
Nie jestem pewien, czy to jest w porządku
drugi punkt podstawiam z przedziału, w którym badamy funkcję
f(4)=4+
√4=6
Zatem funkcja ma według tych obliczeń jedno ekstremum, ale wydaje mi się, że powinny być dwa.
2 lut 21:18
MQ: Coś ci "po krótkich obliczeniach" źle wyszło.
1+12√x >0 dla x∊R\{0}, bo √x>0 dla x∊R\{0}
2 lut 21:24
neocortex: 1.Czy można porównać 1+12√x do zera, czy zawsze będę pisał >0?
2.Ekstremum liczę przyrównując pochodną do 0, prawda?
2 lut 21:33
MQ: Sorry, nie R\{0} tylko R+
2 lut 21:34
MQ: Pochodna zawsze dodatnia, więc funkcja rosnąca ⇒ ekstremum w prawym krańcu przedziału badanego.
2 lut 21:35
neocortex: Czyli w zerze pochodna nie istnieje?
2 lut 21:39
MQ: Nie jest określona
2 lut 21:40
neocortex: A w przypadku ekstremum lokalnego nie ma żadnych rozwiązań?
2 lut 21:43
MQ: Jakiego ekstremum lokalnego?
W tym przypadku jedyne ekstremum jest w x=4
2 lut 21:45
Mila:
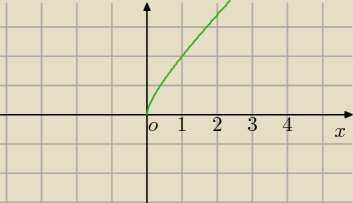
Pochodna f '(x)>0⇔Funkcja rosnąca, liczysz na końcach przedziału
Dla x=0 jest f(0)=0
dla x=4 jest f(4)=4+
√4=6
2 lut 21:46
neocortex: MQ, Chodzi mi, że kiedy byłoby zadanie z ekstremum lokalnym, bez podanego przedziału to nie
byłoby rozwiązań, tak?
2 lut 21:50
neocortex: Według tego wykresu da się funkcję przyrównać do zera, a mi to nie wyszło. Zrobiłem to tak,
proszę o poprawienie:
1+12√x=−1
−1+12√x=1
−2√x=1
−√x=12
x=12√x
2 lut 22:01
MQ: W tym wypadku miałbyś ekstremum −− minimum globalne w 0, bo dziedzina <0,+∞) zawiera jeden
kraniec.
2 lut 22:05
neocortex: Jeszcze raz, bo źle przepisałem:
1+12√x=0
12√x=−1
−12√x=1
−2√x=1
−√x=12
x=12√x
2 lut 22:11
neocortex: To jak wygląda to w formie liczbowej, przyrównując pochodną do zera?
2 lut 22:13
MQ: Ja bym zrobił tak:
| | 1 | |
√x=− |
| <0 ⇒ sprzeczność bo funkcja √x przyjmuje wartości dodatnie ⇒ brak rozwiązań |
| | 2 | |
2 lut 22:13
neocortex: To by znaczyło, że wykres nie osiąga punktu 0?
2 lut 22:16
MQ: Osiąga −− funkcja w tym punkcie ma wartość 0.
Ty przyrównywałeś pochodną do 0 w tym punkcie −− to pochodna w 0 nie istnieje.
2 lut 22:18
Mila:
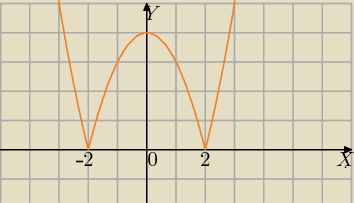
Neocor, czy nie widzisz, że pochodna jest dodatnia?
Ekstrema mogą być w punktach gdzie pochodna nie istnieje.
np.
y=|x
2−4|
Nie istnieje pochodna w x=−2 i x=2 a są tam ekstrema
2 lut 22:23
neocortex: x+√x jest dość trudna do narysowania. Jak mógłbym podać rozwiązanie nie rysując wykresu?
Chodzi mi o egzaminacyjne podejście.
2 lut 22:23
MQ: Nie jest trudna do narysowania
1. Rysujesz √x
2. Obracasz o 45o od osi OX w górę.
2 lut 22:25
MQ: Cofam −− nie do końca tak to jest −− sorry.
2 lut 22:27
neocortex: OK przećwiczę to
2 lut 22:27
neocortex: A jak?
2 lut 22:28
Milax: Zrób tabelkę, narysowałam Ci wykres, wiesz, że rosnąca.
f(0)=0
f(1)=1+√1
f(4)=4+√4 i kilka przybliżeń
2 lut 22:56
neocortex: Ok, dziękuję
3 lut 09:32