rozwiąż równanie i nierówność Karol: Próbuje i próbuje to rozwiązać i same głupoty mi wychodzą może jakaś podpowiedź jak zacząć oba ?

2x + 11		5 − 2x
	−		= 3
2x − 4		2x + 4

x2 + 5		3x −2		3(1−x)
	−		>
x2 −1		x−1		x+1

lila: zaczynasz od dziedziny, potem wspólny mianownik

zombi: w pierwszym podpowiedź

a		c		ad−cb
	−		=
b		d		bc

Karol: zrobiłem tak jak w podpowiedzi do pierwszego i mam

8x2 + 28x + 64
	= 3
4x2 − 16

liczyć delte z mianownika

lila: nie 28x a 12x

Karol : Faktycznie ma być 12x

Karol : ale i tak delta wychodzi na − mi pomimo zmiany

lila: nie delta wychodzi 121, bo musisz ten ułamek pomnożyć stronami przez mianownik

Karol: 8x² + 12x +64 = 3(4x²− 16) − 4x² + 12x + 112 =0 Δ= 1936 ⇒44 mi wyszło tak moze gdzieś mam błąd

Karol: Znajdzie ktoś czas i zerknie to drugiego zadania z nierównością Mała podpowiedź

Mila: x²−1=(x−1)(x+1) wszystko na jedną stronę Sprowadzasz do wspólnego mianownika,

Karol: Zrobiłem w nierówności tak, że ...

x2 + 5		3(1−x)		3x −2
	>		+
x2 − 1		x+1		x − 1

x2 + 5		2x2 + 5x − 5
	>
x2 − 1		x2 − 1

x2 + 5		2x2 + 5x − 5
	−		>0
x2 − 1		x2 − 1

− x2 − 5x +10
	> 0
x2 − 1

nie wiem czy teraz pomnożyć przez mianownik i rozpatrzyć tylko licznik

Karol: Proszę pomóżcie

Mila: Zle licznik z prawej ma być:7x−5 stąd

x2−7x+10
	>0
(x−1)(x+1)

Δ=9 x₁=2 lub x₂=5 (x−2)(x−5)(x−1)(x+1)>0 m. zerowe: −1; 1; 2; 5 cdn

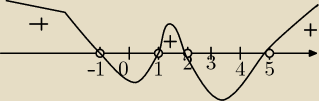
Mila: x∊(−∞;−1)∪(1;2)∪(5;∞)

Karol: Dziękuje ślicznie Mam jeszcze 3 przykłady które musze rozwiązac i chciałbym prosic o wskazówki

26		5		3
	−		=
4x2 −9		2x+3		2x−3

√x²+4< x+2

2		3
	<
x−3		x−2

Milax: 1) dziedzina przenieś ułamek z 5 na drugą strone, potem na krzyż. 2) x+2>0 i podnieś do kwadratu obustronnie 3) na jedną stronę

Karol: 1) zawsze mam problem z tą dziedziną ale zrobiłem tak 2x+3= 0 x = −1,5 2x − 3=0 x= 1,5 4x² −9=0 (2x+3)(2x−3)=0 x=−1,5 i x= 1,5 D = R\{−1,5;1,5}

26		16x −6
	=
4x2 −9		4x2 −9

−16x +32
	=0
4x2 −9

(−16x +32 )
(2x+3)(2x−3)

Karol: 3)

2		3
	−		<0
x−3		x−2

x +5
x2 − 5x + 6

m.zerowe 5, 2,3

Karol: 2)nie rozumiem tego zrobiłem tyle i nie wiem jak dalej √x² +4 < x² + 4 x² + 4 < x² + 4

Karol: Czy coś jest dobrze z tego co napisałem

Karol: Proszę pomóżcie

Mila: 2) x+2>0, bo przecież wartość pierwiastka nie może być mniejsza od zera. x>−2 (√x²+4)²<(x+2)² x²+4< x²+4x+4 ⇔ 0<4x⇔x>0 3)

2		3
	<		mianowniki różne od zera⇔x−3≠0 i x−2≠0⇔x≠3 i x≠2
x−3		x−2

2		3
	−		<0
x−3		x−2

2(x−2)−3(x−3)
	<0
(x−3)(x−2)

−x+5
	<0⇔
(x−3)(x−2)

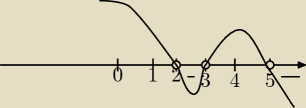
(−x+5)(x−3)(x−2)<0 x=5;x=3;x=2 x∊(2;3)∪(5;∞)

Mila: 1) (−16x +32 )=0 16x=32 x=2

Mila: Zał. do (1) 2x−3≠0 i 2x+3≠0⇔

	3		3
x≠		i x≠−
	2		2

Karol: Dziękuje

Mila: : Pomogło?