pytanie
nie wiem: jak sprawdzic czy funkcja jest roznowartpsciowa? np ta :
2 lut 19:23
Dominik: mozna chociazby narysowac wykres. f(x) jest roznowartosciowa.
2 lut 19:25
Aga1.:
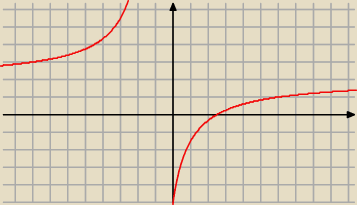
2 lut 19:26
lila: zgodnie z def funkcji różnowartościowej należy wykazać, że jeżeli x1≠x2 i x1, x2 ∊D, to
f(x1)≠f(x2)
2 lut 19:27
Nienor: 1. Z wykresu
2. Z definicji
| | 2(x1+1)−7 | | −7 | |
f(x1)= |
| =2+ |
|
|
| | x1+1 | | x1+1 | |
funkcja nie jest różnowartościowa, jeżeli istnieje x
1≠x
2 spełniające równanie:
| | −7 | | −7 | |
2+ |
| =2+ |
| , a to jest równoważne równaniu:
|
| | x1+1 | | x2+1 | |
x
1+1=x
2+1
A jest ono spełnione tylko wtedy, gdy x
1=x
2, czyli funkcja jest rówżnowartościowa.
2 lut 19:29
nie wiem: czyli wyznaczyc tylko dziedzine ?
2 lut 19:29
Aga1.: Nie wystarczy wyznaczyć dziedziny, to jest początek rozwiązywania.
2 lut 19:30
nie wiem: jak to sie oblicza?
2 lut 19:33
Nienor: Nie rozumiesz tego co napisałam
Jak coś mogę wytłumaczyć.
2 lut 19:34
nie wiem: skad ten zapis w ogole ? ta 7 ?
2 lut 19:39
Nienor: | | 2x−5 | |
Sprwadzam wyrażenie |
| do tzw. postaci kanonicznej, bo akurat w niej więcej widać.
|
| | x+1 | |
Robię to tak:
Tworzę w liczniku coś w nawiasie, takie samo jak w mianowniku, stąd w liczniku: 2(x+1), ale że
z tego wychodzi:2x+2, to żeby całość się zgadała i wynosiła tyle co trzeba odejmuję 7
2 lut 19:46
nie wiem: ok dzieki
2 lut 19:51