. Zuza: Dany jest czworokąt ABCD. Miary kątów przy wierzchołkach A, B, C, D w podanej kolejności tworzą ciag arytmetyczny. Wykaż, że czworokąt ten jest trapezem.

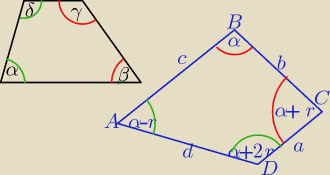
Bogdan: W trapezie α + δ = 180^o i β + γ = 180^o. Ciąg arytmetyczny (a_n): a₁ = α − r, a₂ = α, a₃ = α + r, a₄ = α + 2r, są to miary kątów czworokąta ABCD. α − r + α + α + r + α + 2r = 360^o ⇒ 4α + 2r = 360^o ⇒ 2α + r = 180^o Dodajemy miary kątów czworokąta przylegające do boku b oraz do boku d: α + α + r = 2α + r = 180^o i α − r + α + 2r = 2α + r = 180^o, spełniona jest zależność charakterystyczna dla trapezu. Czworokąt jest więc trapezem.