| arctgx | ||
f(x) = | ||
| 1−arctgx |
| pi | pi | pi | pi | |||||
odpowiedz to : (0; | ) U (− | ; | ) U ( | ; ∞) | ||||
| 4 | 4 | 4 | 4 |
| π | π | π | ||||
tgx=1 dla | oraz − | więcej nie rozpatrujemy bo działamy na przedziale (− | , | |||
| 4 | 4 | 2 |
| π | ||
) | ||
| 2 |
| 1 | π | π | ||||
arctgx z tego co widzę na wiki itd. to | dla x∊(− | , | ), czyli w twojej | |||
| tgx | 2 | 2 |
| 1 | |
≠1 | |
| tgx |
| π | π | |||
tgx=1, gdy x=− | lub x= | , więc wywalasz te iksy z dziedziny, tylko jednego nie | ||
| 4 | 4 |

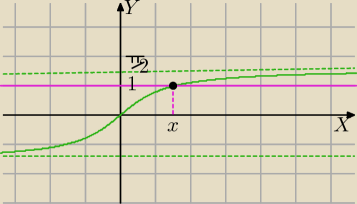 arctgx≠1⇔x≠tg(1)
Popatrz dokładnie na treść zadania i odpowiedź.
arctgx≠1⇔x≠tg(1)
Popatrz dokładnie na treść zadania i odpowiedź.
| 1 | ||
arctgx=1 ⇒ | =1 ⇒ tgx=1? | |
| tgx |
| 1 | ||
zombi ... −1 oznacza funkcję odwrotną a nie | ||
| f(x) |
| 1 | ||
przecież zapis funkcji odwrotnej f−1(x) nie oznacza | ||
| f(x) |
 Bo jak wpisałem w wolframie 'arctan' to jako wyniki dostałem tan−1x, tyle że nie
podałem argumentu i domyślnie było 0, a wtedy na prawdę wychodzi na to samo.
Bo jak wpisałem w wolframie 'arctan' to jako wyniki dostałem tan−1x, tyle że nie
podałem argumentu i domyślnie było 0, a wtedy na prawdę wychodzi na to samo.