Stereometria - obliczanie pola powierzchni brył hekan: Witam mam problem z zadaniem: Krawędź podstawy ostrosłupa prawidłowego trójkątnego wynosi 4, a ściany boczne są nachylone pod kątem 60*, Ostrosłup ten przecięto płaszczyzną równoległą do płaszczyzny podstawy i przechodzącą przez środek wysokości. Oblicz pole powierzchni każdej z otrzymanej brył. próbowałem i nie wychodzi

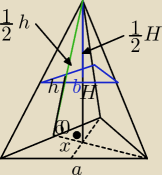
Beti: a = 4

	1		a√3		1		4√3		2√3
x =		*		=		*		=
	3		2		3		2		3

	x
cos60o =
	h

1		2√3   3
	=
2		h

	4√3
h =
	3

	h		1   h 2
z trójkątów podobnych:		=
	1   a 2		1   b 2

	h		h
		=
	2		b

b = 2 GÓRNA BRYŁA:

	b2√3		1		1
Pc =		+ 3*		b*		h
	4		2		2

	3		2√3
Pc = √3 +		*2*
	2		3

P_c = √3 + 2√3 = 3√3 DOLNA BRYŁA:

	a2√3		a+b		1		b2√3
Pc =		+ 3*		*		h +
	4		2		2		4

	3		2√3
Pc = 4√3 +		*6*		+ √3
	2		3

P_c = 4√3 + 6√3 + √3 = 11√3