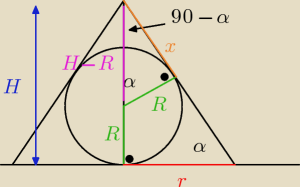
Optymalizacja Nienor: Oblicz największą objętość jaką może mieć stożek opisany na kuli o promieniu R. Różowe to H−R Z: H>2R, H,R,r,x>0 Z podobieństwa trójkątów:

R		r		RH
	=		⇒ r=
x		H		x

z Pitagorasa: x²=(H−R)²+R²=H²−2HR ⇒ x=√H²−2HR

	HR
r=
	√H2−2HR

	1
V=		πr2H
	3

	1		H2R2		1		H2R2
V(H)=		π		*H=		π
	3		H2−2HR		3		H−2R

	1		2H(H−2R)−H2		1		H2−2HR
V'(H)=		πR2		=		πR2
	3		(H−2R)2		3		(H−2R)2

V'(H)>0 ⇔ H²−2HR>0 H(H−2R)>0 V'(H)>0 ⇔ H∊(2R,+∞) V'(H)<0 ⇔ H∊(0,2R) V(H) nie ma maksimum, stożek nie ma objętości największej.

b.: masz błąd przy korzystaniu z tw. Pitagorasa, powinno być x² + (H−R)² = R²

b.: odpowiedź jest mimo to poprawna

+-: Stożek ma objętość "największą" to ∞ (i to 2 razy) co widać na oko, może tu chodzi o stożek wpisany w kulę