.

. pi: rozwiąż równanie

	pi		√3
cos(2x+		)=
	4		2

no i wychodza mi rozwiazania

	−π		−5
x=		+kπ lub x=		+kπ
	12		12

a w odp jest

	−π		−5
x=		+kπ lub x=		+kπ
	24		24

2 lut 12:46

Ajtek:

	π
Po lewej stronie masz cos(2x+		)
	4

Zapewne zgubiłeś tą dwójkę.

2 lut 12:58

pi:

	−2π		−10
nie no doszedlem do wersji 2x=		+2kπ lub 2x=		+2k
	24		24

no i jak sobie obustronnie to skrocilem przez 2 to mam to co wyzej, czyli x=−π/12+kπ lub x=−5/12 +5π

2 lut 13:09

Ajtek: Jak skracasz obustronnie przez 2 to liczniki skracasz, mianownik zostaje emotka

2 lut 13:11

pi: ajjj, dzieki

2 lut 13:12

Ajtek: Powodzenia.

2 lut 13:15

pi: a jak określić dziedzine w takim równaniu? wystarczy ze cos x∊ R?

2 lut 13:40

pi: chodzi mi dokladnie o nowe równanie tg x/2=√3

	π
wystarczy ze x=R\{		+kπ}
	2

2 lut 13:43

Ajtek:

	x		x
Nie. Masz tg		⇒ cos		≠0 i rozwiązujesz
	2		2

2 lut 13:47

pi: a dlaczego tak? Ja to sobie inaczej rozwiazalem i mi sie zgadza, ale chetnie sie dowiem o co chodzi w tym sposobie.

2 lut 13:51

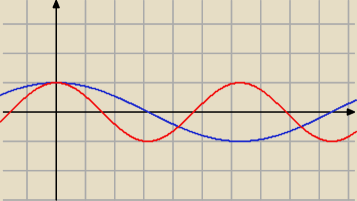
Ajtek: rysunek

	x		π
cos		≠cos(		+kπ)
	2		2

x		π
	≠		+kπ /*2
2		2

x≠π+2kπ czerowny y=cosx

	x
niebieski y=cos
	2

2 lut 13:57

pi:

	x		x
nie czaje jak to sie ma do tg		i jak to zamieniles na cos
	2		2

2 lut 14:08

Ajtek: Wiesz że:

	sinα		π
tgα=		⇔ cosα≠0 ⇒ α≠		+kπ
	cosα		2

	x
U Ciebie α=
	2

2 lut 14:11

pi: teraz juz wiem skad to jest. a dajmy jak mam sin⁵₂x=0 t=5/x sint=x t₀=0 t=0+2kπ lub t=π−0+kπ k∊C

5		5		5		5
	x=0+2kπ\|*		lub		x=π−0+2kπ \|*
2		2		2		2

	2		4
x=⁴₅π, k∊C lub x=		π+		kπ, k∊C
	5		5

ok to jest?

2 lut 14:23

Ajtek: rysunek

Ale kombinujesz

. sinx=0 ⇒ x=kπ

	5		5
sin(		x=0 ⇒		x=kπ
	2		2

Dalej dasz radę.

2 lut 14:26

Ajtek: pi wychodzę na zakupy, będę za godzinę mniej więcej.

2 lut 14:28

pi: bo mam do kazdej funkcji ogolny schemat, np do sinusa x=x₀+kπ lub x=π−x₀+2kπ innego motywu nie znam

2 lut 14:30

Ajtek: Ten sposób na sinα jest dla α∊(0;90), (90;180) itd. Gdy sinα=0 to α=kπ, bo co 180^o sinα przyjmuje wartość 0.

	π
sinα=1 to α=		+2kπ, bo sinα przyjmuje wartość 1 co 360^o
	2

	3
sinα=−1 to α=		π +2kπ, bo sinα przyjmuje wartość również co 360^o
	2

2 lut 15:17

pi: czyli moge sobie to uzywać, a dla szczegolnych przypadkow −1 0 i 1 najlepiej z wykresu, tak?(dla cos i sin oczywiscie)

2 lut 15:22

Ajtek: Dokładnie emotka

2 lut 15:23

pi: a z tg i ctg zawsze x=x₀+kπ?

2 lut 15:24

Ajtek: Yhy emotka

2 lut 15:25

pi: no dobra,czyli z tego przykladu tak jak wyzej pisales

5
	x=kπ
2

	2
x=		kπ?
	5

2 lut 15:29

pi: dobra zgadza sie z odp emotka

dzieki za pomoc

2 lut 15:34

pi: czyli dla cos 2x=−1

	π
bedzie x=		+kπ
	2

2 lut 15:54

pi:

	π
czy jeszcze x=		−kπ?
	2

2 lut 15:56

Ajtek:

	π
x=		+kπ, k∊C, pamiętaj o tym.
	2

2 lut 16:19

pi:

2 lut 16:55

Ajtek: O co chodzi?

2 lut 16:55

pi: nieważne, miałem stronę nieodświeżoną.

2 lut 16:56

Ajtek: Aha emotka

2 lut 16:57

pi: A dajmy jak jest tg4x=−1

3 lut 15:23

pi: tak samo jakby było tg4x=1

3 lut 15:24

pi:

	pi
ogolnie mam pytanie czy jak np jest 2cos(		−x)=−√2
	4

	π
to cos "zjada" minus zawsze, czyli to bedzie		czy U− {π}{4}
	4

Chodzi mi o samo jedno dowolne rozwiazanie

3 lut 15:54

pi: tam mialo byc:

	π		π
to cos "zjada" minus zawsze, czyli to bedzie		czy −
	4		4

3 lut 15:55

pi: odpowie ktos?

3 lut 16:57

Dominik:

	π
2cos(		− x) = √2
	4

	π		p
cos(		− x) =
	4		2

	π		π
kosinus zadnego minusa nie zjada, tylko przyjmuje takie wartosci dla		LUB −
	4		4

	π		π		π		π
czyli		− x =		∨		− x = −
	4		4		4		4

3 lut 17:01

pi:

	π
no ale to i tak wychodzi −x=2kpi lub x=		−2kpi k∊c
	2

	π
a w odp jest x=−		+2kπ lub x=π+2kπ
	2

3 lut 17:57

pi:

3 lut 18:24

pi:

3 lut 18:55

Dominik: jeszcze raz, bo poucinalem odpowiedzi wczesniej.

	π		√2
cos(		− x) =
	4		2

π		π		π		π
	− x =		+ 2kπ ∨		− x = −		+ 2kπ
4		4		4		4

	π
x = −2kπ ∨ x =		− 2kπ
	2

gdzie k∊ℂ sugerowalbym wyrzucic ten zbior zadan nowej ery i kupic jakis porzadny, np autorstwa panstwa "klaczkow, kurczab i swida".

3 lut 20:28

pi: to nawet nie zbiór, to zwykly podrecznik

3 lut 22:19

Dominik: po co ci podrecznik jak masz ta strone? emotka

3 lut 22:24