Geometria płaska - trójkąty
Narufirefox: Mam parę zadań z którymi nie mogę sobie poradzić, pomoże ktoś ?
1. W trójkącie prostokątnym równoramiennym środkowa poprowadzona na przeciwprostokątną ma
długość 6 cm. Oblicz długość środkowej poprowadzonej z wierzchołka kąta ostrego tego trójkąta.
2. W trójkącie równoramiennym największy kąt jest równy 120 st., a najkrótsza wysokość ma 1 dm
długości. Wyznacz promień okręgu opisanego na tym trójkącie.
3. Boki trójkąta mają długość: 16 cm, 10 cm, 10 cm. Oblicz odległość między środkiem okręgu
wpisanego w ten trójkąt a środkiem okręgu opisanego na tym trójkącie.
4. We wnętrzu kąta ostrego leży punkt A. Na jednym ramieniu kąta wyznacz punkt B, a na drugim
ramieniu − punkt C, tak aby obwód trójkąta ABC był najmniejszy z możliwych.
5. We wnętrzu kąta o mierze 60 st. leży punkt S. Odległość punktu S od ramion kąta wynosi
odpowiednio 4√6 i √6. Oblicz odległość punktu S od wierzchołka O tego kąta.
2 lut 11:23
Skipper:
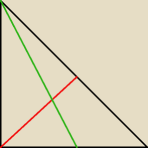
a)
chyba wszystko jasne
2 lut 11:28
Skipper:
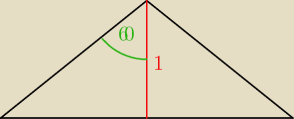
b)
też banał −
2 lut 11:31
Narufirefox: Które zrobiłeś ?
2 lut 11:34
Skipper:
no tak ... le pooznaczałem
1 i 2
2 lut 11:35
Narufirefox: Ale przecież nie ma odpowiedzi tylko rysunki.. o.O
2 lut 11:41
Skipper:
... a to TY czekasz na gotowca
?
2 lut 11:47
Narufirefox: Do tych rysunków to doszedłem ale nie potrafię obliczeń.. :<
2 lut 11:47
Skipper:
W 1)
Skoro ta wysokość (czerwona) ma 6cm .... to przyprostokątne mają
?
A dalej to już Pitagorasek
2 lut 11:57
Skipper:
w 2)
| | a | |
policz podstawę a potem R= |
| |
| | 2sinα | |
2 lut 12:01
Narufirefox: Trygonometrii jeszcze nie miałem ale ok spróbuję.. A następne ?
2 lut 12:41
Narufirefox: To jak będzie z resztą ?
2 lut 13:07
pigor: ...no to masz ...
"gotowce" (lubię je pisać, bo nie są takie oczywiste)
:
1) a
√2= 12 ⇒ a= 6
√2 ⇒ a
2= 72 i x
2=
54a
2=
54*72= 5*18= 9*10 ⇒
⇒
x=3√10 − szukana długość środkowej .
−−−−−−−−−−−−−−−−−−−−−−−−
2) np, tak : niech r,2a długość ramienia i podstawy odpowiednio danego Δ,
to z Δ ekierki :
r=2*1=2, a=1
√3=
√3 ⇒ pole Δ S=
12*2a*1=
√3 ⇒
| | r*r*2a | | 2*2*√3 | |
R= |
| = |
| =2 dm − szukany promień . |
| | 4S | | 2*√3 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
3) np. tak: h=6 wysokość względem podstawy 2*8=16 i pole Δ S=
12*16*6= 48,
zaś połowa obwodu Δ p= 5+5+8=18 , więc
r=Sp=
4818=
83 i
R=10*10*164*48=
5*53=
253, zatem
d=R−(6−r)=
253−(
183−
83)=
153=
5 cm − szukana odległość .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
i na razie tyle ...
2 lut 13:35
Narufirefox: Dzięki
Jak dasz rady jeszcze tamte 2 to będę wdzięczny
2 lut 15:36
matfiz:
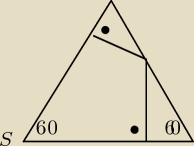
wystarczy twierdzenie o trójkącie 30, 60, 90 oraz twierdzenie pitagorasa i rozwiązane
;>
16 lut 16:43
matfiz: to było do ostatniego zadanka
16 lut 16:44
jozek: 6
26 mar 14:30
jozek:
26 mar 14:30
jozek:
26 mar 14:31
jozek: 7
26 mar 14:31