Pochodna funkcji odwrotnej

Pochodna funkcji odwrotnej asdf: Czy mółby ktoś mi pomóc jak udowodnić pochodną funkcji odwrotnej z definicji

1 lut 21:52

MQ: Funkcji odwrotnej czy odwrotności funkcji?

1 lut 21:54

asdf:

	1
Pochodna funkcji odwrotnej (f⁻¹(y_o))' =
	f'(x₀)

1 lut 22:24

Trivial: (:

1 lut 22:42

Trivial: Naszym argumentem jest y, a nie x. x(y) = f⁻¹(y) Chcemy znaleźć x'(y). Stosujemy obustronnie f. Możemy to zrobić, gdyż f jest odwracalna, czyli f jest też bijekcją (wzajemną jednoznacznością) f(x(y)) = y Różniczkujemy obustronnie (argumentem jest y!) (f(x(y))' = 1 f'(x(y))*x'(y) = 1 Aha! Mamy nasze x'(y).

	1
x'(y) =
	f'(x)

Podstawiając...

	1
(f⁻¹(y))' =		.
	f'(x)

1 lut 22:56

asdf: https://secure.join.me/977-063-756

1 lut 23:02

asdf: wytłumaczysz mi to Trivial?

1 lut 23:02

Mila: Czy już jasne,ASDF ?

1 lut 23:35

asdf: jeszcze nie do konca..mogłabyś dorzucić swoje rozumowanie? (latwiej bym moze to zrozumiał)

2 lut 00:11

Mila: f(x)− funkcja ciągła, różnowartościowa i różniczkowalna w przedziale [a;b] g(x) funkcja odwrotna do f(x) g jest też różniczkowalna; niech f '(x₀} ≠0

	g(f(x))−g(f(x₀))
Lim_x→x₀		= pochodna złożenia funkcji
	x−x₀

	g(f(x))−g(f(x₀))		f(x)−f(x₀)
=lim{x→x₀}		*		=
	x−x₀		f(x)−f(x₀)

	g(f(x))−g(f(x₀))		f(x)−f(x₀)
=lim{x→x₀}		*		=g' o f '⇔
	f(x)−f(x₀)		(x−x₀)

1=g' (y₀)o f'(x₀)

	1
g'(y₀)=
	f '(x₀)

2 lut 00:28

asdf: a dlaczego jest równe 1?

2 lut 00:59

asdf: sorki, musialem sobie to gdzies zapisac: M = − mgr * sinx sinx = x (dla x−>0) M = −mgrx I * ε = − mgrx

	mgrx
ε = −
	I

d²x		−mgrx
	=
dt²		I

	k
ω = √
	m

k = mlg I = m

	2π
T =
	ω

2 lut 03:08

asdf:

	dx
F = −b
	dt

b − wsp. oporu F = −kx − bv x = A₀ * e^−βt * cos(ωt + Φ) β − wsp. tłum drg. tłum − ω₁=√w₀² − β²

	k
częstkość własna ω₀=√
	m

2 lut 03:21

asdf: podbijam, bo nie wiem jak z tą jedynką.

2 lut 13:43

Trivial: Liczysz pochodną (g(f(x)))' = (f⁻¹(f(x)))' = (x)' = 1.

2 lut 13:52

asdf: jakby to się miało na wykresie?

2 lut 14:04

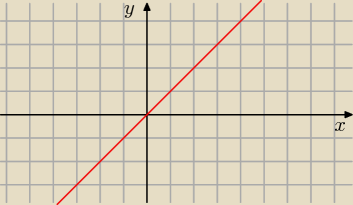
Trivial: rysunek

Na wykresie? Co na wykresie? y = f⁻¹(f(x)) = x.

2 lut 14:07

asdf: moglbys mi tak szybko to jeszcze raz wytlumaczyc? (jeden przyklad starczy): https://secure.join.me/428-999-837

2 lut 14:13

Trivial: Dziś wieczorem (koło 22)

2 lut 14:13

asdf: ok, spoko.

2 lut 14:14

Mila: Widzę, że Trivial mnie wyręczył. Dzięki> emotka

2 lut 15:03

asdf: y = x − względem tej funkcji tworzy się funkcja odwrotna, a pochodna po niej to 1 tak?

2 lut 18:06

Mila: (x)'=1 Złożenie g(f(x))=x Przecież korzystasz z tego np. sin(arcsinx)=x

	1		1
sin(arcsin		)=sin30⁰=
	2		2

2 lut 18:18

asdf: ok, dzięki. Jak sam sobie nie przetłumacze to nie zrozumiem (tak już mam) emotka

2 lut 18:22

Mila: Bardzo dobrze, że jesteś dociekliwy. emotka

A ja nie mogę się pokolorować, ciągle coś mi odrzuca.

2 lut 18:27

asdf: moze sprobuj zalogowac sie ponownie i dopiero

2 lut 18:46

asdf: miałem wszystko zapamiętane, wyloguj się (odswiez strone − moze pomoze, ale juz bardziej by pomoglo wywalenie cache, ale mniejsza z tym) i zaloguj sie ponownie na Twój nick. Jak nie spróbuj odzyskać hasło (jak nie pamiętasz)

2 lut 18:58

asdf: mogłaś sobie dać spację przed nickiem emotka

byłoby nie zauważalne emotka

2 lut 22:28

Trivial: emotka

2 lut 22:52

Trivial: A czy jesteś aby zalogowana?

2 lut 23:00

Mila: Byłam, to jak sprawdzić? emotka

Gdy to piszę to mam kolor różowy, gdy wyślę , to czarny.

2 lut 23:06

Trivial: Spróbuj z innej przeglądarki i zobacz czy da się pokolorować. Jeśli będzie się dało, przyczyną są prawdopodobnie ciasteczka.

2 lut 23:08

asdf: @Trivial, masz chwile troche czasu na elektrycznosc i magnetyzm? (musze wyprowadzic kilka wzoró na ściągę)

2 lut 23:15

Trivial: mam chwilkę, ale trochę jestem śpiący. emotka

Więc nie za długo.

2 lut 23:16

asdf: https://secure.join.me/788-274-076

2 lut 23:17

Mila: Trivial, to było trywialne. Dziękuję. emotka

2 lut 23:33

Trivial: Co było problemem? emotka

2 lut 23:34

Mila: Logowanie. emotka

2 lut 23:35

Trivial: emotka

2 lut 23:37