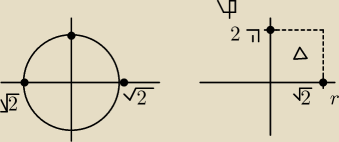
całka Wojtek: Mam do sprawdzenia całkę J=∫∫_D e^x2+y2 dx gdzie x²+y²=2 S(0,0) r=√2

	⎧	x=rcosφ
Φ=	⎩	y=rsinφ

∫∫_Δ e^{−(r2cos2φ + r2sin2φ}*r drdφ= =∫∫_Δ e^−r2 *rdrdφ= =∫₀^√2 (∫₀^2π e^−r2 *r dφ)dr= ∫₀^√2 2πe^−r2 *r=

	r2
=2π∫0√2 e−r2 *rdr= 2πe−r2*		|0√2=
	2

=πe⁻²*2=2πe⁻² <<<<<<<< WYNIK (***) ∫₀^2π e^−r2 *r dφ= e^−r2 *r |₀^2π=2πe^−r2 *r