a może to kogoś zaciekawi??? proszę o pomoc w rozwiązaniu:) ange: wyznacz ekstrema lokalne funkcji f(x)= ln x − x , dla x∊{0,∞} z góry dziękuję

AS: No i jak? Podjęłam próbę dojść do wyniku czy potrzebna jest pomoc.

ange: nie wiem czy dobrze to robię, a nie mam nikogo, kim mogłabym porxównać wyniki, robię to tak: wyliczam najpierw pochodną: (ln x−x)' = (ln x)'− (x)'= 1/x −1 to f(x) = 0 ⇔ 1/x −1=0 ⇔ x=0 f(x) > 0 ⇔ 1/x −1>0 ⇔1/x >1 ⇔ x< 1 max {1} min zbiór pusty czy o to chodziło

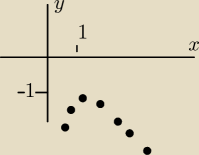
AS: Pochodna wyliczona poprawnie,ale równanie wyliczone błędnie. Wystarczyło podstawić x = 0 do równania by się przekonać że coś nie tak. f'(x) = 0 ⇔ 1/x − 1 = 0 ⇔ (1 − x)/x = 0 ⇔ 1 − x = 0 ⇔ x = 1 f(1) = ln(1) − 1 = 0 − 1 = −1 f'(x) > 0 dla 0 < x < 1 np. f(1/2) = 1/(1/2) − 1 = 2 − 1 = 1 funkcja w (0,1) rośnie bo pochodna przyjmuje wartości dodatnie f'(x) < 0 dla x > 1 np. f(2) = 1/2 − 1 = −1/2 funkcja w (1,∞) maleje bo pochodna przyjmuje wartości ujemne Funkcja przyjmuje maksimum w punkcie W(1,−1)

ange: dziękuję, o to mi chodziło, żeby ktoś mógł powiedzieć czy to co robię jest dobrze, super ,że są tacy ludzie , pozdrawiam serdecznie

AS: Miła Ange (mam nadzieję) Życzę powodzenia na egzaminie. Ściskam kciuki u lewej i prawej ręki. Do następnego poczytania

ange: Jeszcze raz dziękuję, za tydzień kończę matematykę, no i wkraczam w statystykę, oj będzie ciężko:( ale trzeba przetrwać POZDRAWIAM SERDECZNIE

AS: Głowa do góry! Pomożemy.