Matematyka w zastosowaniach Saizou : Dzisiaj odbył się etap szkolny konkursu pn. Matematyka w zastosowaniach i oto pytania (jakby kogoś interesowały) zadanie 1 Na rachunku oszczędnościowym bank kapitalizuje odsetki według nominalnej stopy procentowej 5% w stosunku rocznym. Na konto wpłacona 10 000 zł. Po roku wypłacono 4000 zł, a na koniec drugiego 5000 zł. Jaka kwota była na koncie po 3 latach? zadanie 2 Mamy złom dwóch rodzajów stali: o 20% zawartości niklu i o 40% zawartości niklu. W jakim stosunku trzeba stopić te dwa rodzaje złomu, by otrzymać stal o zawartości niklu od 25% do 30%? zadanie 3 Większa koparka wykonuje pewną pracę P w czasie o 12 dni krótszym niż koparka mniejsza. Razem mogą wykonać tę pracę w 8 dni. Pracowały razem 3 dni, po czym większą koparkę odesłano do innej pracy. Ile dni potrzebuje mniejsza koparka na dokończenie rozpoczętej pracy? zadanie 4 Adam stoi w odległości 70m od podstawy masztu telewizyjnego, a Bolek w odległości 42m od podstawy tego masztu. Odległość między chłopcami wynosi 98m. Ewa stoi na odcinku między nimi w takim punkcie, że widzi wierzchołek masztu pod największym kątem. a) W jakiej odległości od każdego z chłopców stai Ewa b) Ewa widzi wierzchołek masztu pod kątem 60^o. Pod jakimi kątami widzą go Adam i Bolek zadanie 5 Z prostokątnego arkusza blachy o wymiarach 32 cm na 42 cm wycięto w narożnikach równe kwadratu, by po zgięciu blachy otrzymać otwarte pudełko o objętości 3520 cm³. Jakie wymiary będzie miło pudełko o najmniejszej, a jakie o największej powierzchni

Saizou : jest ktoś chętny

pigor: ... , podoba mi się zadanie 2, a widzę je np. tak : niech x,y − masa złomu stali o 20%, 40%−ej zawartości niklu odpowiednio i ^y_x=t=? , to y=tx, a wtedy warunki zadania opisuje np. taka nierówność : 25%(x+tx)< 20%x+40%tx< 30%(x+tx) /:5%x ⇒ 5(1+t)< 4+8t< 6(1+t) /+(−4) ⇔ ⇔ 1+5t< 8t< 2+6t ⇔ 1+5t< 8t i 8t< 2+6t ⇔ 3t >1 i 2t< 2 ⇔ ¹₃< t < 1 ⇔ ⇔ ¹₃< ^y_x < 1 lub odwrotnie 1< ^x_y< 3 − szukane stosunki . ...

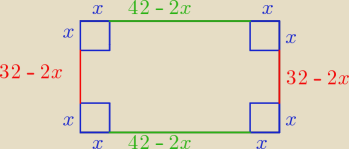
AltXor: Będzię miało: długość: 42 − 2x szerokość: 32 − 2x wysokość: x V = d*sz*w V = (42 − 2x)(32 − 2x)*x (42 − 2x)(32 − 2x)*x = 3520 4x³ − 148 x² + 1344x − 3520 = 0 Mamy wielomian więc szukamy największej i najmniejszej wartości. Nie chce mi się dalej liczyć

AltXor: Co do zadania 3 to skandal Jak można pracę oznaczać jako P! Przecież to W jak wół, ewentualnie mogli wykonać pracę ΔtP... Skandal normalnie...

Saizou : ja tych pytań nie układałem więc to ich wymysł

pigor: ... , o co tak mało chętnych , no to wiidzę np, tak : zad.1, po 1 roku : 105%*10000 zł = 105*100= 10500 − 4000= 6500 zł ; po 2 roku : 105%* 6500 zł = 105* 65= 6500+325= 6825 − 5000= 1825 zł ; po 3 roku : 105%* 1825 zł = 105* 18,25= 1916,25 zł − stan konta po 3 latach. ...

pigor: ..., no to nie mając nic do niej ... , widzę tę pracę np. tak: zad.3, ¹_x−12+¹_x= ¹₈ /*8x(x−12) i 3*¹₈+d*¹_x=⁵₈ i x>12 i d=? ⇒ ⇒ 8x+8(x−12)=x(x−12) i d*¹_x=²₈ ⇔ x²−28x+96=0 i d*¹_x=¹₄ ⇒ ⇒ Δ=400 i x=¹₂(28+20)= 24 i d= 24*¹₄ ⇒ d=6 dni . ...

xxx: Dlaczego w zadaniu 3 jest na końcu 2 równania jest 5/8?