Geometria Sarna: W trapezie kąty ostre przy dłuższej podstawie mają miary 45 stopni i 60 stopni. Krótsza podstawa ma miarę 3cm, a długość krótszego ramienia wynosi 4 √3 cm. Oblicz pole tego trapezu. Wynik mi wychodzi P= 18 + 12√3 + 12√6 ale wydaje mi się że jest źle bo powinna wychodzia normalna liczba.

Janek191: b = 3 cm a = x + b + y d = 4 √3 cm Mamy y/ d = cos 60^o y/ (4 √3) = 1/2 y = 2 √3 −−−−−−−−−−−−−− h = x zatem h² + y² = d² h² = ( 4 √3)² − ( 2 √3)² = 48 − 12 = 36 więc h = √36 = 6 oraz x = 6 zatem a = 6 + 3 + 2 √3 = 9 + 2 √3 Pole trapezu P = 0,5 *( a + b) *h ================ P = 0,5 *( 9 + 2 √3 + 3) * 6 = 3*(12 + 2 √3) = 36 + 6 √3 Odp. P = ( 36 + 6 √3 ) cm² ============================

Magda:

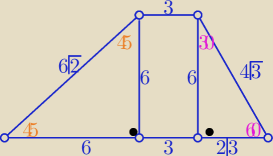
Eta: Z własności trójkatów "ekierkowych" ( dane na rys.) P= 6(6+√3) cm² jak u Janka