Bardzo prosze o dokładne wytłumaczenie. Letty: Podstawy trapezu mają długość 10 i 6. Suma miar kątów wewnętrznych czworokąta przy dłuższej podstawie jest równa 90stopni. Oblicz długość odcinka łączącego środki podstaw oraz środki przekątnych czworokąta. Bardzo prosze o dokładne wytłumaczenie., ponieważ ja wiem że na internecie znajde dokładnie takie samo zadanie, ale nie rozumiem go dobrze, chodzi mi też o inny (może prostszy) sposób zrobienia tego. Od tego zależy moje życie. Z góry dziękuje

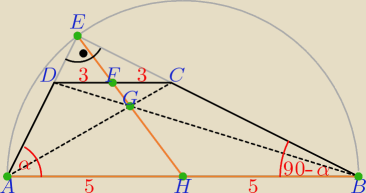
Bogdan: Odcinek EH jest środkową prostokątnego trójkąta ABC i jest i jest jednocześnie równy promieniowi okręgu opisanego na tym trójkącie, |EH| = |AH| = |HB| = 5 Szukamy długości odcinka FH.

	|AB|		|EH|
Korzystając z podobieństwa trójkątów: ABC i DCE:		=
	|CD|		|EH| − |FH|

10		5
	=		, stąd obliczymy długość FH.
6		5 − |FH|

Jeśli w trapezie podstawy mają długości a, b, a > b, to długość odcinka łączącego środki

	a − b
jego przekątnych jest równa
	2

Eta: Myślę,że można też długość |FH| obliczyć tak: Długość odcinka FE jest równa długości promienia okręgu opisanego na trójkącie prostokątnym CDE , |EF|= |DE|=|FC|= 3 to |FH|= |EH|−|EF|= 5−3=2

Mila: Pięknie rozwiązane, dodam: |EF|=|DE|=|FC|

Bogdan: