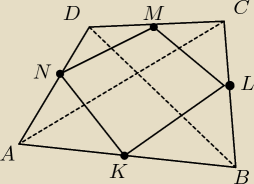
 Mam pytanie co do pewnego zadania, mógłby ktoś powiedzieć czy dobrze myślę? otóż..Wykaż, że w
dowolnym czworokącie wypukłym środki jego boków są wierzchołkami pewnego równoległoboku.
Wpadłem na taki pomysł, że:
|AN|=|ND|
|DM|=|MC|
|CL|=|LB|
|BK|=|KA|
Na podstawie twierdzenia o odcinku łączącym środki boków trójkątów ΔACD i ΔACB, można
zauważyć,że |NM| || |AC|| i |KL| || |AC|⇒|NM| || |KL| oraz |NK| || |DB| i |ML| || |DB| ⇒
|NK| || |ML| ⇒czworokąt KLMN ma dwie pary boków równoległych, więc jest równoległobokiem.....
Mam pytanie co do pewnego zadania, mógłby ktoś powiedzieć czy dobrze myślę? otóż..Wykaż, że w
dowolnym czworokącie wypukłym środki jego boków są wierzchołkami pewnego równoległoboku.
Wpadłem na taki pomysł, że:
|AN|=|ND|
|DM|=|MC|
|CL|=|LB|
|BK|=|KA|
Na podstawie twierdzenia o odcinku łączącym środki boków trójkątów ΔACD i ΔACB, można
zauważyć,że |NM| || |AC|| i |KL| || |AC|⇒|NM| || |KL| oraz |NK| || |DB| i |ML| || |DB| ⇒
|NK| || |ML| ⇒czworokąt KLMN ma dwie pary boków równoległych, więc jest równoległobokiem.....
| 1 | ||
Dopowiadam, że| NM|= | |AC| dalej zobaczysz więcej, bo jesteś myślącą osóbką. | |
| 2 |
