Rozwiąż nierówności wajdzik: Zadanie. Rozwiąż nierówności Witam, mam problem z rozwiązaniem dwóch nierówności. c)5x⁴−1>0 tutaj zrobiłbym tak: t=x² ale po dalszym liczeniu gdzieś się gubię. oraz d)64−x⁶<0 Proszę o zrobienie tych zadań oraz wytłumaczenie. Z góry dziękuję, Pozdrawiam!

Eta:

	1		1		1
1/x4=		⇒ x1= 4√		x2= 4√
	5		5		5

wajdzik: Nie za bardzo rozumiem

PW: Eta zakłada, że coś wiesz.

	1
Oznaczę ten pierwiastek czwartego stopnia z		symbolem a, żeby mi się szybciej pisało.
	5

	1
x4−		=x4−a4=(x2)2−(a2)2 = (x2−a2)(x2+a2)=(x−a)(x+a)(x2+a2)
	5

Nierówność

	1
x4−		>0 jest zatem równoważna nierówności
	5

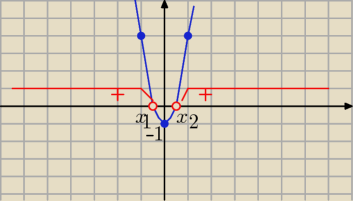
(x−a)(x+a)(x²+a²)>0, a ponieważ x²+a²>0 dla każdej x, można tę nierówność podzielić stronami przez (x²+a²) nie zmieniając nierówności na przeciwną, czyli zadana nierówność jest równoważna następującej: (x−a)(x+a)>0. To masz na rysunku: parabola (niebieska) i zaznaczone (czerwonym kolorem) przedziały stanowiące rozwiązanie. Matematycy w takiej sytuacji piszą "jak łatwo widać". dla Ety.

Eta: