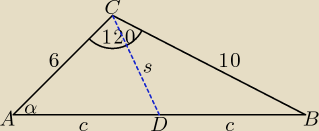
planimetria środkowa trójkąta Dvain: W trójkącie ABC dane są |AC| = 6, |BC| = 10 i |∠ACB|=120 stopni. Wyznacz długość środkowej CD i długość promienia okręgu opisanego na trójkącie.

Bogdan:

	√3
c > 0, cos120o = cos(180o − 60o) = −cos60o = −0,5, sin120o = sin60o =
	2

Z tw. cosinusów: w ΔABC: 4c² = 100 + 36 + 2*6*10*0,5 = 196 ⇒ 2c = 14 w ΔABC: 100 = 36 + 196 − 2*6*14cosα ⇒ cosα = ... w ΔADC: s² = 36 + 49 − 2*6*7*cosα

	2c
Z tw. sinusów w ΔABC:		= 2R ⇒ R= ...
	sin120o

Dominik: myslisz, ze dvain do teraz czekal na rozwiazanie?

Bogdan: Nie, ale rozwiązanie zadania może przydać się innym

Bartek: Przydało się. Dzięki.