 W = √4x2+12x+9 + 2*√x2−12x+36 = √(2x+3)2 + 2*√(x−6)2 = |2*x + 3| + 2*|x − 6|
x dla x ≥ 0
Przypominam: |x| =
−x dla x < 0
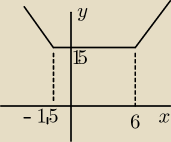
Miejscami zerowymi wyrażeń w wartościach bezwzględnych są −3/2 i 6
Wobec tego rozpatrzyć należy przedziały (−∞,−3/2),<−3/2,6>, (6,∞)
W (−∞,−3/2) wyrażenie 2*x + 3 przyjmuje wartości ujemne,wobec tego |2*x + 3| = −(2*x + 3) =
−2*x − 3
w tym samym przedziale wyrażenie x − 6 przyjmuje też wartości ujemne czyli |x − 6| = −(x − 6) =
−x + 6
W = −2*x − 3 + 2*(−x + 6) = −2*x − 3 − 2*x + 12 = −4*x + 9
W (−3/2,6) wyrażenie 2*x + 3 przyjmuje wartości dodatnie,wobec tego |2*x + 3| = 2*x + 3 = 2*x +
3
w tym samym przedziale wyrażenie x − 6 przyjmuje wartości ujemne czyli |x − 6| = −(x − 6) = −x
+ 6
W = 2*x + 3 + 2*(−x + 6) = 2*x + 3 − 2*x + 12 = 15
W (6,∞) wyrażenie 2*x + 3 przyjmuje wartości dodatnie,wobec tego |2*x + 3| = 2*x + 3
w tym samym przedziale wyrażenie x − 6 przyjmuje też wartości dodatnie czyli |x − 6| = x − 6
W = 2*x + 3 + 2*(x − 6) = 2*x + 3 + 2*x − 12 = 4*x − 9
Przedział w zadaniu zawiera się w przedziale (−3/2,6), tym samym wartość wyrażenia
wynosi 15 dla każdego x z przedziału.
W = √4x2+12x+9 + 2*√x2−12x+36 = √(2x+3)2 + 2*√(x−6)2 = |2*x + 3| + 2*|x − 6|
x dla x ≥ 0
Przypominam: |x| =
−x dla x < 0
Miejscami zerowymi wyrażeń w wartościach bezwzględnych są −3/2 i 6
Wobec tego rozpatrzyć należy przedziały (−∞,−3/2),<−3/2,6>, (6,∞)
W (−∞,−3/2) wyrażenie 2*x + 3 przyjmuje wartości ujemne,wobec tego |2*x + 3| = −(2*x + 3) =
−2*x − 3
w tym samym przedziale wyrażenie x − 6 przyjmuje też wartości ujemne czyli |x − 6| = −(x − 6) =
−x + 6
W = −2*x − 3 + 2*(−x + 6) = −2*x − 3 − 2*x + 12 = −4*x + 9
W (−3/2,6) wyrażenie 2*x + 3 przyjmuje wartości dodatnie,wobec tego |2*x + 3| = 2*x + 3 = 2*x +
3
w tym samym przedziale wyrażenie x − 6 przyjmuje wartości ujemne czyli |x − 6| = −(x − 6) = −x
+ 6
W = 2*x + 3 + 2*(−x + 6) = 2*x + 3 − 2*x + 12 = 15
W (6,∞) wyrażenie 2*x + 3 przyjmuje wartości dodatnie,wobec tego |2*x + 3| = 2*x + 3
w tym samym przedziale wyrażenie x − 6 przyjmuje też wartości dodatnie czyli |x − 6| = x − 6
W = 2*x + 3 + 2*(x − 6) = 2*x + 3 + 2*x − 12 = 4*x − 9
Przedział w zadaniu zawiera się w przedziale (−3/2,6), tym samym wartość wyrażenia
wynosi 15 dla każdego x z przedziału.
 Znowu mam z głowy podawanie uzasadnienia do tego zadania .
Znowu mam z głowy podawanie uzasadnienia do tego zadania . Miłego dnia!
Miłego dnia!
 . Ja jednak podam rozwiązanie tego zadania, mimo, że As już to zrobił.
. Ja jednak podam rozwiązanie tego zadania, mimo, że As już to zrobił.
 Nie wiem czemu ?..... nie spojrzałam ,że to As je podał
Nie wiem czemu ?..... nie spojrzałam ,że to As je podał 
 Wykonujemy tylko te działania i obliczenia, które są potrzebne do rozwiązania zadania.
Wykonujemy tylko te działania i obliczenia, które są potrzebne do rozwiązania zadania.
| 3 | ||
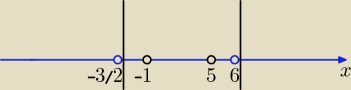
y = |2x + 3| + 2|x − 6| ⇒ y = 2|x + | | + 2|x − 6|. | |
| 2 |
| 3 | ||
Dla x ∊ (−1, 5) ⊂ (− | , 6>: y = 2x + 3 − 2x + 12 ⇒ y = 15 co należało wykazać. | |
| 2 |
 ...... i o to chodziło!
bez zbędnych .....dodatkowych obliczeń.
...... i o to chodziło!
bez zbędnych .....dodatkowych obliczeń.