. asdf: granice funkcji

	∨
limx−>x0 f(x) = g ⇔		[limn→∞ xn = x0 ⇒ f(xn) = g]
	xn∊ S(x0)

może ktoś mi wytlumaczyć to dokładnie działa i jak się to czyta? jaki związek ma tutaj granica ciągu (i dlaczego przy n−> inf)?

asdf: ?

Artur_z_miasta_Neptuna: dla każdego ciągu x_n takiego ... że x_n zbiega do x₀ zachodzi f(x₀) = g ewentualnie powinno być lim_{xn −> x0} f(x_n) = g

asdf: tylko dlaczego jest to granica ciągu? (x_n) Jak to ma się na wykresie?

asdf: mógłby mi ktoś pomóc w zrozumieniu tej definicji?

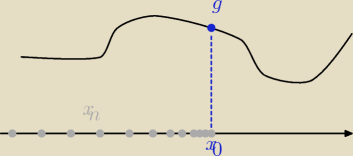
Artur_z_miasta_Neptuna: rysunek obrazujący sytuację

Artur_z_miasta_Neptuna: na przykładzie wykazać, że lim_x−>2 x² = 4 tworzymy ciągi x_n takie, że lim_n−>∞ x_n = 2

	1
(przykładowo xn = 2−		−−− uwaga ... w definicji jest "dla każdego" więc to co
	n

piszę nie jest rozwiązaniem zadania a tylko ilustracją 'jak to działa') z tego wynikać ma, że lim_n−>∞ f(x_n) = 4 (dla tego konkretnego ciągu będziemy mieć)

	1		1
limn−>∞ (xn)2 = limn−>∞ (2 −		)2 = limn−>∞ 4*(1−		)2 = 4
	n		2n

Artur_z_miasta_Neptuna: tak działa definicja Heinego ... ale jak widzisz ... jest to okropna definicja jeśli chodzi o wykazanie istnienia granicy w punkcie ... łatwiej wykazać jej brak (wybierasz dwa ciągi zbiezne do x₀ dla których f(x_n) będą zbiegać do innych wartości)

asdf: Dziękuję Ci bardzo za wyjaśnienie. Masz racje − okropna definicja, do zrozumienia łatwa nie jest.