przedzialy monotonicznosci iLoveMath: Hej, mam do zbadania przedziały monotoniczności takiej funkcji

	|x2−7x+10|
f(x)=
	x−1

x₁=5 x₂=2

	⎧	x2−7x+10 dla x∊(−∞, 2>∪<5, ∞)
i teraz dlaczego |x2−7x+10|=	⎨
	⎩	−(x2 − 7x + 10) dla x∊(2, 5)

? ok to teraz dalej pochodne dla każdego przypadku 1. x²−2x−3 x₁=−1 x₂=3 2. −x²+2x+3 x₁=−1 x₂=3 obie parabole przecinaja oś w tych samych miejscach zerowych, z tym że ramiona jednej skierowane są w górę, a drugiej w dół. co w takim przypadku ?

Skipper: ... policzyłeś tylko miejsca "zerowania" pochodnych. Zauważ jednak, że musisz każdorazowo sprawdzić czy mieszczą się one w rozpatrywanych przedziałach ... (w pkt.1 x=3 poza przedziałem ... zaś w pkt.2 x=−1 poza przedziałem) ... więc zmianę znaku rozpatruj w odpowiednich przedziałach −

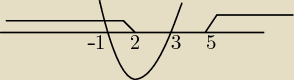
iLoveMath: a co z dziedziną jjeśli jest R\{1} ? bo w 1 przypadku gdy x∊(−∞,2>∪<5,∞) f(x)>0 dla x∊(−∞, −1)∪(5,∞) f(x)<0 dla x∊(−1,2) tak to ma być

iLoveMath: ?

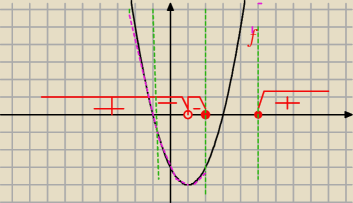
Aga1.: Zwróć uwagę, że do dziedziny nie należy 1 Rozpatrujesz dwa przypadki 1)Dla x∊(−∞,2>U<5,∞)/{1} Funkcja f przyjmuje postać

	x2−7x+10
f(x)=
	x−1

Pochodna

	(2x−7)(x−1)−(x2−7x+10)		x2−2x−3
f'(x)=		=
	(x−1)2		(x−1)2

Wykres pochodnej (licznika) Na podstawie wykresu pochodnej podajesz przedziały monotoniczności f↗(−∞,−1) f↗<5,∞) f↘(−1,1) f↘(1,2) Rozpatrz podobnie drugi przypadek.

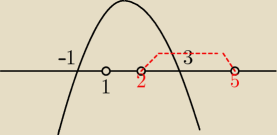
iLoveMath: ok, więc pochodna w drugim przypadku to −x²+2x+3 x₁=−1 x₂=3 rozpatruje dla przedziału x∊(2,5)\{1} więc f(x)↗ dla x∊(2.3) f↘ dla x∊(3,5) tak ?

iLoveMath: a jak zapisać odpowiedź dla całej funkcji ?

iLoveMath: czy to będzie f↗ dla x∊(−∞,−1)∪<5,∞)∪(2.3) f↘(−1,1)∪(1,2)∪(3,5)

iLoveMath: ?

Aga1.: Odp. Przepisz moją i dopisz swoją.(6 linijek) Nie sprawdzałam Twoich obliczeń .Rozpatrujesz w przedziale (2,5), bo 1 do tego przedziału nie należy. Przy monotoniczności nie łącz przedziałów sumą

iLoveMath: Przy monotoniczności nie łącz przedziałów sumą ja już sam nie wiem co mam robić, profesor na ćwiczeniach tak pisał to i ja tak pisze a takie pytanie bo chyba błąd zrobiłem w pochodnej w 2 przykładzie dla

	(−2x+7)(x−1)−(x2+7x−10)
u('{−x2+7x−10}{x−1})'=		=
	(x−1)2

	−2x2+2x+7x−7−x2−7x+10
		=
	(x−1)2

	−3x2+2x+3
=		?
	(x−1)2

Aga1.:

	−x2+7x−10		(−2x+7)(x−1)−(−x2+7x−10)		−x2+2x+3
(		)'=		=
	x−1		(x−1)2		(x−1)2

Z tym przedziałami przy monotoniczności tak jest, że czasami można połączyć je sumą mnogościową , a czasami nie. Jak nie wiesz, czy można, czy nie można , to po prostu ich nie łącz i już.