symetralna odcinka mati: wyznacz rownanie symetralnej odcinka o koncach A(−2,2)B(2,10)

bash: Wzór na równanie symetralnej odcinka możesz znaleźć w tablicach maturalnych

lila: np. C(x,y) jest dowolnym punktem należącym do symetralnej i wtedy zachodzi warunek AC=BC i wyliczasz z tego warunku y=...

bash: przepraszam rozpędziłem się...w tablicach znajdziesz wzór na środek

	xA+xB		yA+yB
odcinka...(		;		)...1)wyznacz równanie prostej przechodzącej przez punkt
	2		2

A i B, załóżmy y 2)symetralna będzie prostą prostopadła do y i przechodzącą przez środek odcinka AB

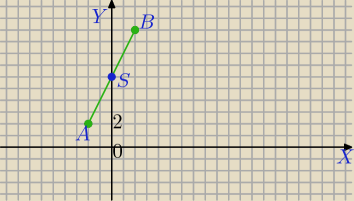
Mila: A(−2,2); B(2,10)

	−2+2		2+10
S=(		;		)=(0;6)
	2		2

prosta AB: y=ax+b b=6 i A∊prostej 2=a*(−2)+6⇔−2a=−4 ⇔a=2 y=2x+6 Symetralna

	−1
s:y=		x+6 (a1*a2)=−1
	2

Aga1.: Inny sposób . Punkt P(x,y) należy do symetralnej odcinka AB, gdy IAPI=IBPI/² IAPI²=IBPI² (√(x+2)²+(y−2)²)²=(√(x−2)²+(y−10)²)² x²+4x+4+y²−4y+4=x²−4x+4+y²−20y+100 16y=−8x+96

	−1
Odp.y=		x+6.
	2