wysokosc 3kata rownoramiennego Dominik: Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, w których stosunek długości wynosi 3 : 5. Oblicz długość ramienia trójkąta. czy ktos jest w stanie wyjasnic mi czemu w odpowiedziach rozpatrzony jest tylko przypadek, ze jest to wysokosc opuszczona na jedno z ramion? wydaje mi sie, ze rownie dobrze moze byc to wysokosc opuszczona na podstawe.

Mila: Właśnie nie może być mowy o wysokości opuszczonej na jedno z ramion , bo środek okręgu opisanego na Δ leży na przecięciu symetralnych boków. Jeśli wysokość zawarta w symetralnej ramienia to oznacza , że Δ jest równoboczny, a jak Ci wiadomo wtedy środek okręgu dzieli wysokość w stosunku 1:2.

Dominik: dzieki. z geometrii do matury jeszcze duzo bede meczyl. mam problemy nawet w podstawa.

Mila: Myślę,że nie jest tak źle, jak piszesz.

Dominik: to moze na boku takie sprawdzenie: Pole trójkąta równoramiennego jest równe 25. Oblicz długość promienia okegu wpisanego w trójkąt wiedząc, że ramię jest dwa razy dłuższe od podstawy. zadanie jest z podstawy, a ja uzywalem jedynki trygonometrycznej, ktora jest wiedza z rozszerzenia ⇒ czyli pewnie zaszalalem wiecej i za duzo kombinowalem w tym zadaniu.

	P		10
oznaczylem podstawe jako x, ramiona jako 2x. wiec r =		=
	p		x

	1
policzylem kosinus kata miedzy podstawa a ramieniem =		, po czym zamienilem na sinus. P =
	4

	1		10
		x2sinα = 25 ⇒ x =		. podstawiajac do rownania z r otrzymuje prawidlowy
	2		4√15

wynik: r = ⁴√15. nie przekombinowalem? podobnie w poprzednich zadaniach, wydaje mi sie ze przekombinowalem i moze dalo sie cos innego zauwazyc. z drugiej strony moze przesadzam i wszystko robie jak najbardziej prawidlowo.

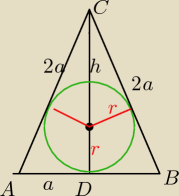
Mila: Można tak: P=25

	1
(2a)2=(		a)2+h2
	2

	1		3		15
h2=4a2−		a2=3		a2=		a2
	4		4		4

	√15
h=		a
	2

1		√15
	a*		a=25
2		2

a²√15=100 a=.. porównanie pól: porównujesz sposoby i wybierasz.

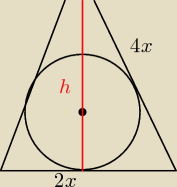
Aga1.: r=U{P_tr{p}, gdzie p połowa obwodu. h²=16x²−x² h=√15x

	1
P=		*2x*√15x
	2

x²√15=25

	5
x=
	4√15

p=5x r=⁴√15

Aga1.:

	Ptr
r=
	p

Dominik: czyli w zasadzie to samo, kwestia uzycia innego wzoru na pole. dzieki.

Kamcio :) : jeśli chodzi o geometrię to akurat moim zdaniem trudniejsza jest podstawa niż rozszerzenie....za dużo tych twierdzen jest na rozszerzeniu Widzę takie zadanie z podstawy, myślę sobie, tu twierdzenie sinusów, tutaj wzór herona, inne cuda niewidy, a potem sie okazuje że wystarczyło twierdzenia pitagorasa użyć