funkcje liniowe kasia: Narysuj wykres funkcji f a następnie podaj ZW, Mo, max. przedziały monotoniczności. f(x) = { −2 dla x<−1 } { x² dla x≥−1 } nie wiem nawet od czego zacząc...

tn: Jak narysujesz to wszystko zobaczysz! No więc masz oś X. I dla x<−1 dajesz −2 Zaś dla x>=−1 dajesz x² Wiesz jak to?

kasia: niestety nie za bardzo...

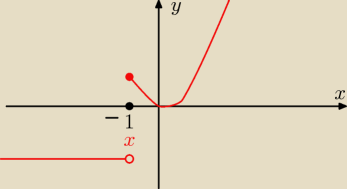
tn: Widzisz teraz: Minimum: −2 Maksimum nie da rady określić. ZW: <0;+∞) ∪ { −2} Jest stała x∊(−∞;−1) maleje: <−1;0) rośnie: <0;+∞)

kasia: to wyżej to jest parabola z tego x² dla x≥ −1

tn: tak

tn: (fragment paraboli)

kasia: a jak wyliczyć z tego miejsca zerowe?

tn: 0 = x² x=0

kasia: jak to wyliczyles, za f(x) podstawiles 0?

tn: Pytanie czym jest miejsce zerowe? ARGUMENT dla którego funkcja osiąga WARTOŚĆ ZERO f(x) jest wartością w zależności od x Pytając o miejsce zerowe popatrz: Zgodnie z definicją pytasz dla jakiego argumentu funkcja osiąga zero więc, zapiusejsz: f(x) = 0 (znaczy tyle samo, co dla jakiego argumentu(x) funkcja osiąga wartość zero) f(x)= 0 x²=0 x=0

kasia: ok nie rozumiem jeszcze zapisu ZW. dlaczego jest <0;+∞) ∪ {−2} ?

tn: ZW, czyli zapis zbiór wartości. Przeciwidziedzina inaczej. A skoro przeciwdziedzin∪a, to nie odczytujemy jej na osi X, tylko Osi Y. Gdzie są pokryte punkty na Osi Y ? Czy wartość (nie argument!) −1 jest zaznaczona na wykresie ? Nie. A co oznacza sam zapis. <0 − to wiesz dlaczego. znaczek '∪' oznacza sumę. Dołączamy jeszcze element −2, bo istnieje taka warotść(funkcją ją przyjmuje)

kasia: no teraz rozumiem dziękuje