calka Wojtek: Mam do sprawdzenia całkę J=∫∫_D e^−(x2+y2) dxdy gdzie D: x²+y²=2

⎧	x=rcosφ
⎩	y=rsinφ

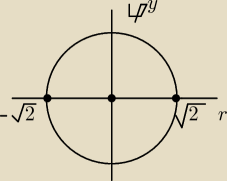
weglug rysunku granice całkowania to: 0<r<√2 0<φ<2π ∫∫_Δ e^{−((rcosφ)2+(rsinφ)2)} * r drdφ= = ∫₀^√2 (∫₀^2π r*e^−(2r2)dφ) dr= >.>∫₀^2π r*e^−(2r2) dφ= = r*e^−(2r2) |₀^2π = =2π r*e^−(2r2)

	r2
∫0√2 2π r*e−(2r2)dr=2π		*e−(2r3 /3)=
	2

= π r²*e^{−(2r3 /3)} |₀^√2 = 2πe^−{4√2/3} Mam przeczucie że coś zwaliłem ale nie wiem co

Krzysiek: e^{−x2 −y2}=e^−r2

Wojtek: ale ja tam nie mam e^−x2−y2 . Mam (rcosφ)²+(rsinφ)² co daje mi jedynke trygonometryczną >> 1*2r²