najmniejsza i największa wartość funkcji!!! Ola: Znajdź najmniejszą i największą wartość funkcji y= 2x²+2x−4 w przedziale: a) <0,1/2> b) <−1, 1 1/2>

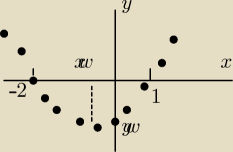
AS: Uwaga: maksimum funkcji nie musi być wartością największą funkcji w przedziale minimum funkcji nie musi być wartością najmniejszą funkcji w przedziale y = 2*x² + 2*x − 4 Δ = 2² − 4*2*(−4) = 4 + 32 = 36 , √Δ = √36 = 6 x1 = (−2 − 6)/4 = −2 , x2 = (−2 + 6)/4 = 1 Położenie wierzchołka xw = −b/(2*a) = −2/(2*2) = −1/2 , yw = −Δ/(4*a) = −36/(4*2) = −−9/2 By rozstrzygnąć problem należy w przedziale ustalić: maksimum i minimum (jeżeli istnieją) i wartości na krańcach przedziału a) przedział <0,1/2> y(0) = 2*0² + 2*0 − 4 = −4 y(1/2) = 2*(1/2)² + 2*1/2 − 4 = 1/2 + 1 − 4 = −2 1/2 Wierzchołek paraboli znajduje się poza przedziałem Wartość najmniejsza y = −4 dla x = 0 Wartość największa y = −2 1/2 dla x = 1/2 b) przedział < −1,3/2> y(−1) = 2*(−1)² +2*(−1) − 4 = 2 − 2 − 4 = −4 y(3/2) = 2*(3/2)² + 2*3/2 − 4 = 9/2 + 3 − 4 = 7/2 Wierzchołek paraboli mieści się w przedziale <−1,3/2> Wartość najmniejsza i zarazem minimum y = −9/2 dla x = −1/2 Wartość największa y = 7/2 dla x = 3/2

Bogdan: Mała uwaga. Nie ma potrzeby wykonywać obliczeń zbędnych. W przypadku wyznaczania najmniejszej oraz największej wartości funkcji kwadratowej w określonym przedziale <x₁, x₂>, najpierw wyznacza się x_w wierzchołka paraboli i jeśli: a) x_w ∊ <x₁, x₂> to wyznacza się y_w = f(x_w), b) x_w ∉ <x₁, x₂> to nie wyznacza się y_w. Np. w przykładzie a)

	1		2
y = 2x2 + 2x − 4 i x ∊ <0.		>, xw = −		∉ <x1, x2>
	2		4

Nie obliczamy y_w, Δ, a już nieporozumieniem jest obliczanie miejsc zerowych. Obliczamy: f(0) = −4, to jest wartość najmniejsza

	1		1		1		1
f(		) = 2*		+ 2*		− 4 = −2		, to jest wartość największa.
	2		4		2		2

AS: W zasadzie zgadzam się z uwagami,chociaż te niby zbędne obliczenia szkody nie przynoszą. (utrwalenie materiału) Miejsca zerowe wyliczałem by naszkicować wykres funkcji a i trochę co niektórym respondentom przypomnieć jak się oblicza miejsca zerowe.

Eta: ....

Bogdan: No Asie, szkody nie przynoszą, ale po co? W ten sposób można by jeszcze dopisać np. postać kanoniczną i iloczynową funkcji, określić jej monotoniczność i podać jeszcze kilka innych informacji − dla utrwalenia materiału. W tym gąszczu wiadomości bezpośrednie rozwiązanie zadania jest mało widoczne i dla czytającego taki zapis odpowiedzi staje się nieczytelny.