zadanie Baśka: W okręgu o środku s wpisany jest trójkąt równoramienny ABC o kącie między ramionami AC i BC równym 40 stopni. Przez wierzchołek Bi środek okęgu S poprowadzono prostą, która przecięła bok AC trójkąta w punkcie D/ Wyznacz miarę kąta CDB.

Baśka: proszę bardzo o pomoc

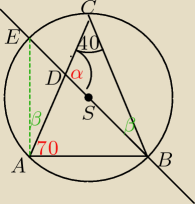
Beti: kąt EAB jest prosty, bo jest oparty na średnicy, więc: kąt EAD = β = 90^o − 70^o = 20^o kąty EAC i EBC są równe, bo to kąty wpisane w okrąg oparte na tym samym łuku na koniec: z sumy kątów w trójkącie CDB mamy: α = 180^o − (40^o + 20^o) = 120^o

Baśka: dzięki