obraz ada: Witam, mam do funkcji f([−2,−1]) znalezc obraz jak to zrobic?

ada: w zeszycie mam zapisane cos takiego, ze z jakiegos wzoru licze f(−1)=1+3+2=6 f(−2)=4+6+2=12 ale nie mam pojecia co to za wzor i o co w tym wogole chodzi

ada: prosze o wytlumaczeniae

ada: pomocy, bardzo mi na tym zalezy

ada: ?

Trivial: Obraz to po prostu... f(X) = { f(x) : x ∊ X} Bez wzoru nie pójdzie..

ada: no wlasnie a ja nie wiem jak to wzor, no nie mam go w zeszycie

ada: i taki rysunek mam do tego , tez nie wiem z kad sie wzial

Trivial: No to przykro mi, ale się nie da bez wzoru tego rozwiązać. Zaprezentuję na przykładzie: f(x) = x² Powiedzmy że szukamy obrazu f w zbiorze X = {−2,−1,0,1,2} mamy: f({−2,−1,0,1,2}) = {f(−2), f(−1), f(0), f(1), f(2)} = {4, 1, 0, 1, 4} = {0, 1, 4} Dla dziedzin niedyskretnych wyznaczenie obrazu odbywa się inaczej. Nie możemy po prostu policzyć wartość funkcji dla każdego elementu dziedziny, gdyż tych elementów jest nieskończenie wiele. 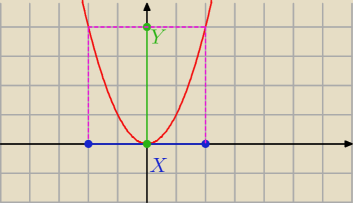Najłatwiej wtedy to narysować: f([−2,2]) = [0,4].

Trivial: Z rysunku można odczytać obraz, wtedy rzeczywiście nie potrzeba wzoru.

ada: tylko tutaj najpiew ona chyba wyliczala ze wzoru a potem rysunek, trudno, sprobuje jakos to rozgryźć

ada: a czemuf([−2,2]) = [0,4].

Trivial: Popatrz na rysunek zbiór X = [−2,2] zbiór f(X) = Y = [0,4]

ada: aha, juz wiem no tak,glupia jestem,dzieki

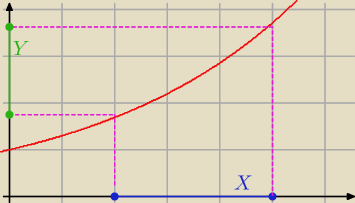
Trivial: Może jeszcze jeden przykład, na którym lepiej widać. f(x) = a^x f([2,5]) = [a², a⁵] na tym wykresie, a = 1.3

ada: nom, juz wiem o co chodzi, dziekuje a mozesz mi powiedziec jeszcze co to znaczy ze funkcja jest "na"?to znaczy ze jst na calym y?

ada: tak po rysunkach wykombinowalam tak na moj rozum

Trivial: Funkcja "na" to inaczej suriekcja. Oznacza to nic więcej niż: Każdy y∊Y należy także do obrazu funkcji. Inaczej: każdy element y ∊ Y można uzyskać stosując f dla jakiegoś x ∊ X Przykład: Niech f: X → Y oraz f(x) = x² wtedy f: [−1,1] → [0,1] jest suriekcją, gdyż każdą liczbę z [0,1] można uzyskać podnosząc do kwadratu jakąś liczbę z [−1,1]; f: [0,1] → [0, 2] nie jest suriekcją, gdyż istnieje na przykład liczba 2∊[0,2], której nie da się uzyskać podnosząc jakąś liczbę z [0,1] do kwadratu. f: R → R₊ jest suriekcją, gdyż każdą liczbę z R₊ można uzyskać podnosząc do kwadratu jakąś liczbę z R.

Trivial: Jeszcze inaczej: f: X → Y jest suriekcją, gdy Y = f(X).