logarytm zuzka: ln2 to w przybliżeniu ile?

sushi_ gg6397228: masz kalkulator?

zuzka: no tak

Dominik: to go uzyj!

Dominik: mozesz tez wpisac w google: ln 2

sushi_ gg6397228: to wpisz "2" a potem nacisnij "ln" −−> tak zrob na kalkulatorze w komputerze

Krzysiek: albo znając rozwinięcie funkcji ln w szereg: zacząć liczyć: 1−1/2+1/3−1/4+1/5−....

PW: ln1<ln2<lne 0<ln2<1

	1
Można więc śmiało powiedzieć, że ln2 to w przybliżeniu		− czyli według Krzyśka suma
	2

pierwszych dwóch wyrazów rozwinięcia. Pytanie "ile to w przybliżeniu" jest na tyle nieprecyzyjne, że zawsze można odpowiedzieć "milion". Dowcip tkwi w odpowiedzi na pytanie "z jaką dokładnością". Tylko nie krzyczcie na mnie, że się wymądrzam, pojawiają się tu ponuracy, dla nich więc od razu mówię: to dowcip.

zuzka: za długo już siedze nad matmą i najprostsze rzeczy jak poszukanie kalkulatora wydaja sie skomplikowane xD dzięki

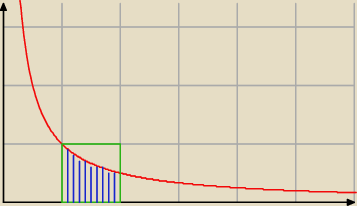
Trivial: Inna metoda:

	1
Wiadomo, że ln(x) = ∫1x		du
	u

	1
Czyli ln(2) = ∫12		du
	u

	3
Z obrazka widać, że jest to jakieś		powierzchni kwadratu. Kwadrat na obrazku ma pole 1,
	4

zatem

	3
ln(2) ≈
	4

PW: @Trivial: Piekne . Muszę już się wyłączyć, bo zaczynam się rechotać, to chyba zły objaw.