PROSZE POMOC MI snave: Wyznaczyć przedziały monotoniczność i ekstrema lokalne funkcji f(x)=2x − e⋀2x + 3

AS: f(x) = 2*x − e^{2*x + 3} Pierwsza pochodna f'(x) = 2 − 2*e^{2*x + 3} Przedziały wzrastania f'(x) > 0 ⇔ 2 − 2*e^{2*x + 3} > 0 ⇔ − 2*e^{2*x + 3} > −2 ⇔ 2*e^{2*x + 3} < 2 ⇔ e^{2*x + 3} < 1 ⇔ e^{2*x + 3} < e⁰ ⇔ 2*x + 3 < 0 ⇔ x < −3/2 Funkcja wzrasta w przedziale (−∞,−1.5) Przedziały malenia f'(x) < 0 ... jak poprzednio ... x > −3/2 Przedziały malenia: (−1.5,∞) Ekstrema f'(x) = 0 ... jak poprzednio ... 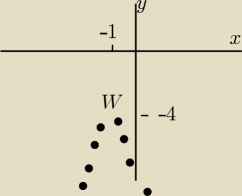x = −1.5 Wartość maksimum: y = 2*(−1.5) − e⁰ = −3 − 1 = −4 Ponieważ pochodna przy przejściu przez x = −1.5 zmienia znak z + na − w W wystepuje maksimum. Wierzchołek W(−1,−4)

Mikołaj: f(x)=2 − e⋀(2x) −3 D=R Pochodna funkcji; f ' (x)= 2 − 2e⋀(2x) =2{1−e⋀(2x)} D ' =R miejsce zerowe pochodnej funkcji; f'(x)=0 ⇔ 1−e⋀(2x)=0 ⇔ e⋀(2x)=1⇔ e⋀(2x)=e⋀(0) ⇔ 2x=0 ⇔ x=o Znaki zerowe; f '(x)>0 ⇔ 1−e⋀(2x)>o ⇔ e⋀(2x)<1 ⇔ e⋀(2x)<e⋀(0) ⇔ 2x<0 ⇔ x<0 f '(x)<0 ⇔ x>0 funkcja jest rosnąca w przedziale (−∞,o],malejąca w przedziale [o,+∞ ) w punkcie x=0 funkcja osiąga maximum lokalne :y=f(0)=2

sylwia gdańsk: ekstrema lokalne funkcj o cholera 1 raz slysze

Mikołaj: