Na jutro:(((((((( k.king199: Oblicz odległość środka ściany bocznej sześcianu od przekątnej sześcianu.

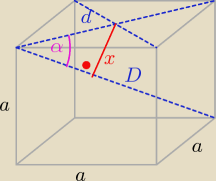
dero2005: d = a√2 D = √a² + d² = a√3

a		√3
	= sin α =
D		3

x
	= sin α
d   2

	d		√6
x =		sinα = a
	2		6

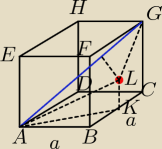PuRXUTM: Kiedyś robiłem to zadanie tym sposobem ale było źle może ktoś wskaże błąd jeśli jest

	1
a2+(		a)2=|AK|2
	2

	√5
|AK|=		a
	2

	1
IKLI=		a
	2

	5		1		6
|AL|2=		a2+		a2=		a2
	4		4		4

|AL|=U{√6{2}a |GL|=U{a√2{2} |FL|=x |AG|=a√3 |AF|=z |FG|=a√3−z i teraz z twierdzenia pitagorasa |AF|²+|FL|²=|AL|² |FL|²+|FG|²=|LG|² |FL|²=|AL|²− |AF|² |FL|²+|FG|²=|LG|² |AL|²− |AF|² +|FG|²=|LG|²

6		1
	a2−z2+ (a√3−z)2=		a2
4		2

3		1
	a2−z2+3a2−2√3az+z2=		a2
2		2

	2√3a
z tego z=		i podstawiamy do
	3

|AF|²+|FL|²=|AL|²

4		3
	a2+|FL|2=		a2
3		2

	1
|FL|2=		a2
	6

	√6
|FL|=		a
	6