n Beata17: Oblicz długość promienia okręgu wpisanego w trapez równoramienny, w którym iloczyn długości podstaw jest równy 16.

Eta: Pomagam rysuję .... cierpliwości

Bogdan:

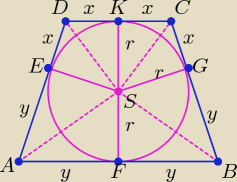
	x		r
Trójkąty CGS i BGS są podobne, stąd mamy proporcję:		=		⇒ r = √xy
	r		y

Bogdan: Witam Eto i przepraszam, że nie uprzedziłem o wejściu w to zadanie.

Beata17: Dzięki

Eta: a*b= 16 h= 2r trapez jest opisany na okręgu , więc zachodzi warunek: a +b = k + k

	a +b
to 2k= a+b => k =
	2

	a −b
ponad to jest równoramienny to: x =
	2

z tw. Pitagorasa w trójkacie AED mamy: k² = x² + h² zatem: h² = k² − x² h² = [¹₂(a+b)]² − [¹₂(a −b)]²

	a2 +2ab +b2 −a2 +2ab − b2
to h2 =
	4

h² = a*b długość h jest średnią geometryczną podstaw h² = 16 => h= 4 ponieważ h= 2r => 2r = 4 => r=2 PS: długość średnicy okręgu wpisanego w trapez równoramienny jest średnią geometryczną długości podstaw trapezu

Eta: Witaj Bogdanie! Podałam nieco inne rozwiązanie .... też poprawne

Eta: Oczywiście z rysunkami nigdy Ci nie dorównam