geometria analityczna
agata zzz: znajdź współrzędne punktu Q będącego obrazem punktu P(−1, −4) w symetrii osiowej względem
prostej k: 5x+4y−20=0
27 sty 23:29
agata zzz: proszę pomóżcie, bo nie wiem co z tym zrobić:(
27 sty 23:41
Eta:
Jak to co?....rozwiązać

27 sty 23:42
agata zzz: faktycznie

fajnie gdybym wiedziała jak wydaje mi się że trzeba wyznaczyć prostą prostopadłą
do te przechodzącą przez punkt P, a dalej nie mam pomysłu:(
27 sty 23:49
Mila:
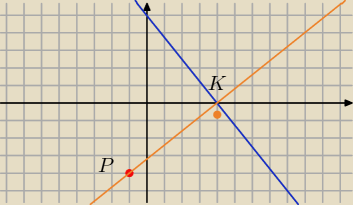
k: 5x+4y−20=0⇔4y=−5x+20 zielona prosta
Piszemy równanie prostopadłej
| | 4 | | 4 | | 1 | |
m⊥k : y= |
| x+b i P∊m⇔−4= |
| *(−1)+b⇔b=−3 |
| |
| | 5 | | 5 | | 5 | |
znajdź współrzędne punktu K i skorzystaj z tego, że K jest środkiem PQ.
27 sty 23:56
Eta:
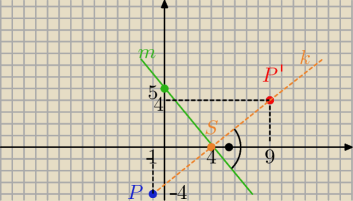 P'(9,4)
P'(9,4)
27 sty 23:59
Eta:
Mila gdzie ta "
zielona" prosta?

28 sty 00:00
pigor: ,..., np. tak: niech
P' =(x,y)=? − szukany obraz punktu P=(−1,−4) i prosta
l ⊥ k : 5x+4y−20=0 przez dany punkt
P=(−1,−4) ma równanie
:
4x−5y+C=0 i 4*(−1)−5*(−4)+C=0 ⇒ C=−16 i
l: 4x−5y−16=0 , więc ich punkt przecięcia
z układu : 5x+4y−20=0 /*5 i 4x−5y−16=0 /*4 ⇔ 25x+20y−100= 0 i 16x−20y−64 /+ stronami
⇒ 41x−164=0 i 4y=20−5x ⇔ x=4 i y=0, czyli
S=(4,0) , zatem ze wzorów na środek
odcinka PP' masz równania : x−1=2*4 i y−4=2*0 ⇔ x=9 i y=4 , więc
P'=(9,4) − szukany
obraz punktu P w symetrii względem danej prostej k . ...

28 sty 00:06
Eta:
I jak ładnie pasuje do mojego rysunku

28 sty 00:08
pigor: ...

faktycznie , dzięki
Eta
28 sty 00:11

 fajnie gdybym wiedziała jak wydaje mi się że trzeba wyznaczyć prostą prostopadłą
do te przechodzącą przez punkt P, a dalej nie mam pomysłu:(
fajnie gdybym wiedziała jak wydaje mi się że trzeba wyznaczyć prostą prostopadłą
do te przechodzącą przez punkt P, a dalej nie mam pomysłu:(
 k: 5x+4y−20=0⇔4y=−5x+20 zielona prosta
k: 5x+4y−20=0⇔4y=−5x+20 zielona prosta
 P'(9,4)
P'(9,4)



 faktycznie , dzięki Eta
faktycznie , dzięki Eta