Funkcja kwadratowa
Dawid:
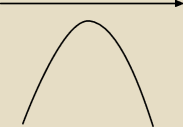
Równanie y= −½x² + 2bx −8, dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży pod osią OX.
Mam problem w tym zadaniu.
Najpierw wyznacza ze Δ<0 więc robię tak
2b
2 − 4 * (−
12) * (−8) < 0
wychodzi
2b
2 − 16 < 0
więc to
b
2 − 4 < 0
więc
(b − 2)(b + 2) < 0
więc miejsca zerowe to
x
1 = 2
x
2 = −2
Wykres mi wychodzi tak jak narysowałem, więc dla mnie to wychodzi ze x należy do zbioru liczb
rzeczywistych w odp jest, że x (−2; 2) − nie wiem wogóle skąd to się wzięlo, proszę o
wytłumaczenie
27 sty 13:25
Skipper:
już na starcie błąd ... przy liczeniu Δ ... b2 .... to (2b)2 czyli 4b2
27 sty 13:28
Skipper:
... a to chyba przy przepisywaniu ..
27 sty 13:30
Dawid: Czyli będzie
(2b)2 −4 * (−12) *(−8) < 0
czyli
4b2 − 16 <0
czyli
b2 − 4 <0
czyli
(b−2)(b+2) < 0
czyli
x1 = 2
x2 = −2
Nie wiem tylko jak ten zbiór policzyć.. na to patrzeć.
27 sty 13:31
Skipper:
... przecież masz analizować Δ ... bo to Δma być mniejsza od 0
27 sty 13:31
Dawid: no, ale to jest delta przecież... przeanalizowałem to.
Δ<0
i pod Δ wzór podstawiłem.
27 sty 13:32
Dawid: aa chodzi, ze w wykresie funkcji mam oprzeć się na delcie, a nie wspolczynnik a patrzec z
funkcji tylko z delty?
27 sty 13:34
Dawid:
proszę o pomoc

Bo jak w tym zadaniu patrzę na współczynnik a z nierówności delty, który jest
dodatni, no to mi wychodzi. Ale w drugim zadaniu podobnym:
Równanie y = 4x
2 − bx + 1 dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży nad osią OX.
i robię tak
Δ<0
b
2 − 4 * 4 * 1 < 0
b
2 − 16 < 0
(b−4)(b+4) < 0
więc
x
1 = 4
x
2 = −4
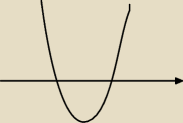
no i tu rysunek jest taki, gdzie punkty styczne to −4 i 4
ale wierzchołek ma być nad osią więc nie rozumiem. w odp wychodzi ze x należy do (−4 ; 4)
27 sty 13:45
 Równanie y= −½x² + 2bx −8, dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży pod osią OX.
Mam problem w tym zadaniu.
Najpierw wyznacza ze Δ<0 więc robię tak
2b2 − 4 * (−12) * (−8) < 0
wychodzi
2b2 − 16 < 0
więc to
b2 − 4 < 0
więc
(b − 2)(b + 2) < 0
więc miejsca zerowe to
x1 = 2
x2 = −2
Wykres mi wychodzi tak jak narysowałem, więc dla mnie to wychodzi ze x należy do zbioru liczb
rzeczywistych w odp jest, że x (−2; 2) − nie wiem wogóle skąd to się wzięlo, proszę o
wytłumaczenie
Równanie y= −½x² + 2bx −8, dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży pod osią OX.
Mam problem w tym zadaniu.
Najpierw wyznacza ze Δ<0 więc robię tak
2b2 − 4 * (−12) * (−8) < 0
wychodzi
2b2 − 16 < 0
więc to
b2 − 4 < 0
więc
(b − 2)(b + 2) < 0
więc miejsca zerowe to
x1 = 2
x2 = −2
Wykres mi wychodzi tak jak narysowałem, więc dla mnie to wychodzi ze x należy do zbioru liczb
rzeczywistych w odp jest, że x (−2; 2) − nie wiem wogóle skąd to się wzięlo, proszę o
wytłumaczenie
 proszę o pomoc
proszę o pomoc  Bo jak w tym zadaniu patrzę na współczynnik a z nierówności delty, który jest
dodatni, no to mi wychodzi. Ale w drugim zadaniu podobnym:
Równanie y = 4x2 − bx + 1 dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży nad osią OX.
i robię tak
Δ<0
b2 − 4 * 4 * 1 < 0
b2 − 16 < 0
(b−4)(b+4) < 0
więc
x1 = 4
x2 = −4
no i tu rysunek jest taki, gdzie punkty styczne to −4 i 4
ale wierzchołek ma być nad osią więc nie rozumiem. w odp wychodzi ze x należy do (−4 ; 4)
Bo jak w tym zadaniu patrzę na współczynnik a z nierówności delty, który jest
dodatni, no to mi wychodzi. Ale w drugim zadaniu podobnym:
Równanie y = 4x2 − bx + 1 dla dowolnej liczby rzeczywistej b, opisuje pewną parabolę. Wyznacz
wszystkie wrtości parametru b, dla których wierzchołek paraboli leży nad osią OX.
i robię tak
Δ<0
b2 − 4 * 4 * 1 < 0
b2 − 16 < 0
(b−4)(b+4) < 0
więc
x1 = 4
x2 = −4
no i tu rysunek jest taki, gdzie punkty styczne to −4 i 4
ale wierzchołek ma być nad osią więc nie rozumiem. w odp wychodzi ze x należy do (−4 ; 4)