ciaglosc asisa: Przypuśćmy, że funkcja ψ: [0,1]→ R jest ciągła, ψ(0)=0 oraz ψ(1)=3 . Wykazać, że równanie (ψ(x))² −3ψ(x) +2 =0 ma co najmniej dwa rozwiązania. bardzo prosze o pomoc w rozwiazaniu tego zadanie

asisa: i te rozwiązania nalezą do przedziału (0,1)

asisa: niech ktos pomoze proszeeeeeee

Kamcio :) : t=φ t²−3t+2=0 (t−2)(t−1)=0 t=2 ⋁ t=0 czyli φ=0 i φ=2 teraz masz podane, że φ(0)=0, 0 należy do danego przedziału więc rozwiązaniem będzie x=0, następnie masz φ(x)=2, funkcja jest ciągła (nie wiem, jestem w drugiej liceum, ale prawdopodobnie można wywnioskować jakoś że jest też rosnąca), czyli φ(x)=2 znajduje się gdzieś w przedziałe (φ(0),φ(1)) a więc x∊(0,1) czyli znaleźliśmy dwa rozwiązania należące do tego przedzialu, ale może ktoś to sprawdzi

asisa: czy to jest dobrze?

Kamcio :) : źle, znalazłem błąd , nie wiem dlaczego tak napisałem ale rozwiązaniami równania będzie t=1 lub t=2

Kamcio :) : aczkolwiek rozumowanie powinno być podobne, skoro funkcja jest ciągła na danym przedziale. Ok, tak się składa że mam akrtkę o ciągłości funkcji. Jest tam twierdzenie Darboux o przyjmowaniu wartości pośrednich, którego założenia są spełnione (funkcja jest ciągła na przedziale [0,1] oraz φ(0)<φ(1), to dla każdego w∊(φ(0),φ(1)) istnieje takie c∊(0,1) , że f(c)=w. W tym przypadku w mamy (z rozwiązania równania) =1 lub w=2, należy do zadanego przedziału, więc wiemy na pewno że dla każdego z tych w istnieje takie c, które należy do przedziału (0,1), co oznacza że funkcja ma conajmniej dwa pierwiastki w tym przedziale

asisa: ty na pewno jestes w drugiej liceum?

Kamcio :) : tak

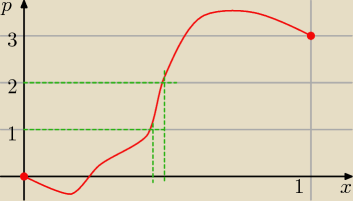
Trivial: Na rysunku p oznacza ψ asisa, tutaj masz prostszą interpretację: 1. Skoro funkcja jest ciągła na przedziale [0,1] oraz ψ(0) = 0, ψ(1) = 3, to funkcja ψ musi osiągać wszystkie wartości pomiędzy [0,3] (patrz rysunek) 2. Zapisujemy równanie w postaci: ψ² − 3ψ + 2 = 0 (ψ−2)(ψ−1) = 0 czyli ψ(x) = 1 lub ψ(x) = 2 Czy istnieją takie x, że ψ(x) jest 1 lub 2? Tak. Jakbyśmy tej funkcji nie narysowali to i tak będzie przynajmniej jeden x taki że ψ(x) = 1 oraz przynajmniej jeden x taki że ψ(x) = 2. Zatem równanie ψ² − 3ψ + 2 = 0 to ma przynajmniej dwa rozwiązania. 3. Te rozwiązania należą do przedziału (0,1), gdyż ψ(0) = 0 nie spełnia równania, a ψ(1) = 3 również go nie spełnia.