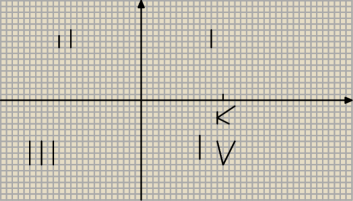
funkcja f określona wzorem f(x)=ax+b jest malejaca toryk: funkcja f określona wzorem f(x)=ax+b jest malejaca a jej miejscem zerowym jest liczba dodatnia.Przez które ćwiartki układu współrzędnych przechodzi wykres tej funkji? Domyślam się że funkcja ta przecinajac sie w punkcie k(miejsce zerowe) przechodzi przez II I i IV(II,bo jest malejaca). Tylko nie wiem jak to uzasadnić?

Dominik: chociazby rysujac szkic takiej funkcji.

toryk: czyli podstawić sobie kilka pktow pod x i y .tzn "tabelka",ta?

Dominik: nie. po prostu poprowadz prosta w ukladzie wspolrzednych, ktory wyzej narysowales. oczywiscie taka, o ktorej mowa w zadaniu − malejaca z dodatnim miejscem zerowym. kazda taka prosta bedzie przechodzila tylko przez te cwiartki.

Artur_z_miasta_Neptuna: prosta f(x) =ax + b jest malejąca ... czyli ma postać: f(x) = −ax + b ; gdzie a>0 skoro dla k>0 zachodzi: 0 = −a*k + b ⇒ b>0 tak więc masz postać: f(x) = −ax+b gdzie a,b>0 gdy x<0 to f(x) = −a*x + b = 'ujemna'*'ujemny x' + liczba dodatnia > 0 stad wniosek −−−− prosta nie przechodzi przez III ćwiartkę

Artur_z_miasta_Neptuna: to jest taki 'pseudo' dowód ... ale zapewne by wystarczył taki

Artur_z_miasta_Neptuna: możesz też poprzestać na stwierdzeniu ... że skoro miejsce zerowe jest dla x₀ > 0 i funkcja ta jest malejąca ... to prosta przecina oś OY w dodatniej jej części (stąd b>0) ... jako że jest to funkcja malejąca ... to wraz coraz mniejszym 'x' wartość funkcji będzie coraz większa ... czyli dla x<0 ... f(x) > b > 0 stąd ... f(x) nie przechodzi przez III ćwiartkę

Kamcio :) : chyba jednak lepiej bedzie narysowac xD