Punkty A = (−1,−2) i C = (3, 4) W: Punkty A = (−1,−2) i C = (3, 4) są przeciwległymi wierzchołkami równoległoboku ABCD. Jeden z jego boków zawiera się w prostej AB o równaniu x − 2y − 3 = 0, a drugi jest zawarty w prostej BC o równaniu 3x + 2y − 17 = 0. Wyznacz współrzędne pozostałych wierzchołków tego równoległoboku i oblicz jego obwód.

Franek: Zderz dwie proste, AB i BC − otrzymasz punkt B. Postępuj analogicznie dla punktu D (i równoległości wobec D). Powodzenia. A w ogóle, to kup sobie Everest Renaty Bednarz.

Janek191: A = ( − 1; − 2), C = ( 3; 4) pr. AB : x − 2y − 3 = 0 czyli 2y = x − 3 y = 0,5 x − 1,5 −−−−−−−−−−−−−−−−−−−− pr. BC : 3x + 2y − 17 = 0 czyli 2y = − 3x + 17 y = − 1,5 x + 8,5 −−−−−−−−−−−−−−−−−−−− Te proste mają wspólny punkt B. 0,5 x − 1,5 = − 1,5x + 8,5 2 x = 10 x = 5 −−−−−−− y = 0,5*5 − 1,5 = 2,5 − 1,5 = 1 −−−−−−−−−−−−−−−−−−−−−−− więc B = ( 5; 1) ============ Przez punkt A prowadzimy prostą równoległą do pr BC : y = − 1,5 x + b1 − 2 = −1,5*(−1) + b1 − 2 −1,5 = b1 b1 = − 3,5 y = −1,5 x − 3,5 − pr.AD −−−−−−−−−−−−−−−−−− Przez punkt C = ( 3; 4) prowadzimy prostą równoległą do pr. AB : y = 0,5 x + b2 4 = 0,5*3 + b2 4 − 1,5 = b2 b2 = 2,5 y = 0,5 x + 2,5 − pr. CD −−−−−−−−−−−−−−−−−−−− Te proste przetną się w punkcie D − 1,5 x − 3,5 = 0,5 x + 2,5 2x = −6 x = − 3 −−−−−−−−− y = 0,5*(−3) + 2,5 = − 1,5 + 2,5 = 1 −−−−−−−−−−−−−−−−−−−−−−−−−−−− więc D = ( − 3;1) ============

Eta: Rozwiązując układ równań AB: x − 2y−3=0 BC: 3x+2y−17=0 −−−−−−−−−−−−− 4x= 20 ⇒ x=5 to y=1 B (5,1) → → → → AB= DC AB= [6,3] , DC=[3−x_D, 4−y_D] to: 3−x_D=6 i 4−y_D= 3 ⇒ x_D= −3 i y_D= 1 D(−3,1)

Eta: Ob= 2(|AB|+|BC|)= .........

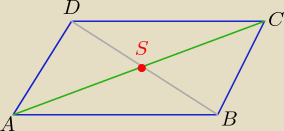
Eta: 3 sposób ( bez wektorów) Przekątne równoległoboku dzielą się na połowy to:

	xA+xC		yA+yC
S(		,		)=.....= S(1,1)
	2		2

to x_D= 2x_S−x_B i y_D= 2y_S−y_B B(−5,1) x_D= 2−5= −3 i y_D= 2−1=1 D(−3, 1)