Ekstrema Kasia : Pomocy Mam jutro kolokwium: wyznacz ekstreme funkcji: f(x)=xe^x

Artur_z_miasta_Neptuna: A z czym studentka ma problem nie zna teorii/"procedury" to do notatek zaglądamy swoich z ćwiczeń i wykladów nie wychodzi jej to pisze nam tu swoje obliczenia 'zacina się' znowu −−− pisze obliczenia inny problem jaki konkretny prosimy

fsfsddfsfsd: 1. Dziedzina D=R 2. Pochodna f'(x)=e^x + xe^x f'(x)=e^x(1+x) e^x − zawsze dodatnie 3. Sprawdzasz kiedy pochodna wieksza mniejsza rowna 0 f'(x)=0 wtedy i tylko wtedy gdy 1+x=0 bo e^x jest zawsze dodatnie wiec x=−1 f'(x)>0 dla x>−1 f'(x)<0 dla x<−1 4. Liczysz asymptoty ( nie chce mi sie, wychodze zaraz ) 5. rysujesz tabelke z charakterystycznymi punktami i przedzialami miedzy tymi punktami czyli (−nieskonczonsc;−1) | −1 | (−1;1) | 1 | (1; + niesk. ) no i wpisujesz wartosci dla punktow a dla przedzialow wpisuejsz czy pochodna jest + czy −

	−1
generalnie odpowiedz to min=max=		dla −1
	e

Kasia : Artur z miasta neptuna chodzi o to ze nie było mnie wtedy na wykładzie i nie mam nic

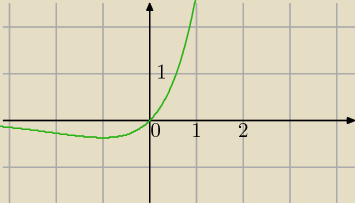
Mila: 1)f(x)=x*e^x D=R 2) miejsca zerowe x*e^x=0 ⇔x=0 i f(0)=0 3)granice na krańcach dziedziny lim_x→∞(x*e^x)=∞

	x		1
limx→−∞(x*ex)=0 [limx→−∞		=H=limx→−∞		=0]
	e−x		−e−x

4)Monotoniczność funkcji i ekstrema f ' (x)=e^x+xe^x f ' (x)=0⇔e^x(1+x)=0⇔x=−1 f ' (x)>0 ⇔1+x>0⇔x>−1 funkcja rosnąca dla x<−1 f. malejąca x=−1 min

	−1
f(−1)=(−1)e−1=
	e

5) punkty przegięcia f ''(x)=e^x+e^x+xe^x=2e^x+xe^x 2e^x+xe^x=0 x+2=0⇔x=−2 2e^x+xe^x>0 ⇔x+2>0; x>−2 dla x=−2 ma punkt przegięcia