prosze o pomoc emotka: stereometria Postprzez emotka » Dzisiaj, 18:09 1. Długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego wynosi 2 a wysokość tego ostrosłupa również 2. oblicz długość krawędzi bocznej, wysokość ściany bocznej, pole powierzchni bocznej oraz objętość. 2. Podstawą graniastosłupa prostego jest romb o boku a i kącie między bokami alfa. Kat pomiędzy przekątną graniastosłupa i jego podstawą jest równy beta. W tym graniastosłupie a = 0,5 alfa = 120 beta = 30 stopni. Oblicz pole powierzchni całkowitej , pole powierzchni bocznej oraz objętość graniastosłupa. 3. Trójkąt prostokątny obracamy dookoła przeciwprostokątnej. Długości przyprostokątnych wynoszą 5 i 3. Oblicz objętość i pole powierzchni całkowitej bryły.

Buc Kipic: 1. Obliczmy wysokosc sciany bocznej: H− wysokosc ostroslupa = 2 a − krawedz podstawy = mamy podane 2 hp−wysokosc podstawy hp=a √3 /2 hp=2 √3 /2 hp=√3 1/3hp=1 √3 /3 hb−wysokosc sciany bocznej hb²=(1 √3 /3)² + 2² hb=√39/3 Obliczmy teraz krawedz boczna: 2/3hp=2 √3 /3 takze z twierdzenia pitagorasa liczymy k− krawedz boczna k²= (2 √3 /3)² + 2² k=√48/3 Obliczmy objetosc Pp = a² √3 /4= √3 v=1/3 * Pp *H v=1/3 * √3 * 2 = 2 √3/3 Obliczmy pole boczne: Pc= Pp + Pb Pc= √3 + 3 * 1* √39/3 Pc = √3 + √39

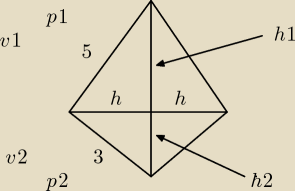
Buc Kipic: 3. h trojkata prostokatnego wynosi h = ab/c a i c to przyprostokatne a przeciwprostokatna to c obliczmy c c= √34 wiec h =15/ √34 czyli promien powstalej figury wynosi tyle co h z twierdzenia pitagorasa liczymy h1 i h2 h1= 25/ √34 h2 = 9 √34 Obliczmy Vc=V1 + V2 V1 liczmy majac podane h1 i h z V1=1/3 * h1*h V2 liczymy V2=1/3 *h2*h Obliczmy Pc=P1 +P2 P1=π h * 5 P2=π h * 3

pigor: ... no to np. 3) dany trójkąt prostokątny po obrocie "daje" 2 stożki "sklejone" podstawami (kołami) o wspólnym promieniu r=? będącym zarazem wysokością danego Δ prostokątnego względem przeciwprostokątnej , tworzących długości L=5 , l=3 i o sumie wysokości tych stożków H₁+H₂=√3²+5²= √34 równej długości przeciwprostokątnej tego trójkąta , zatem z warunków zadania i porównania wzorów na pole Δ prostokątnego masz równanie ¹₂√34*r= ¹₂*5*3 ⇔ √34*r= 15 ⇔ r= ¹⁵₃₄√34 , więc V_b= ¹₃π r²*H₁+¹₃π r²H₂= ¹₃π r²(H₁+h₂)=

	152		15		75
= 13π		*√34= 5π		√34=		π √34 j3. − objętość,
	34		34		34

	15		15
natomiast Pc=π rL+π rl= πr(L+l)= π*		√34(5+3)=		π √34 j2. − szukana
	34		17

powierzchnia całkowita powstałej bryły . ...