opis Geniusz: Okrąg o promieniu 4cm jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków tego trójkąta na odcinki długości 6cm i 8cm . Oblicz długości boków trójkąta.

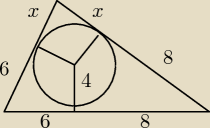
Geniusz: nie wiem jak obliczyć x

Janek191: Pole trójkąta P = 0,5 * [ 4*( x + 8) + 4*(6 + 8) + 4*( x + 6)] = 2*(x + 8) + 2*14 + 2*( x + 6) = = 2x + 16 + 28 + 2x + 12 = 4x + 56 Obliczam teraz pole z wzoru Herona 2p = 2x + 2*6 + 2*8 = 2x + 12 + 16 = 2x +28 / : 2 p = x + 14 −−−−−−−−−−−−−−−− p − a = x + 14 − ( x + 8) = 6 p − b = x + 14 − 14 = x p − c = x + 14 − ( x + 6) = 8 zatem P = √ p*( p − a)*( p − b) * ( p − c) = √ ( x + 14)*6*x*8 = = √48x*( x + 14) Mamy więc √ 48 x*( x + 14) = 4x + 56 ; podnosimy do kwadratu 48 x² + 672 x = 16 x² + 448 x + 3 136 32 x² + 224 x − 3 136 = 0 / : 32 x² + 7 x − 98 = 0 −−−−−−−−−−−−−−−−−−−− Δ = 7² − 4*1* ( −98) = 49 + 392 = 441 √Δ = 21 x = ( − 7 + 21)/2 = 14/2 = 7 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 8 + 7 = 15 6 + 7 = 13 6 + 8 = 14 Odp. Boki tego trójkąta mają długości: 15, 14, 13. ==========================================

Eta:

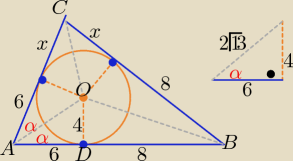
Eta: Można też tak:

	2√13		3√13
sinα=		, cosα=
	13		13

	12
sin2α= 2sinα*cosα= .... =
	13

	7*12(6+x)
P(ΔABC)= 7*(6+x)*sin2α=
	13

	1
P(ΔABC)= r(		Ob)=4(14+x)
	2

7*12(6+x)
	= 4(14+x) ⇒ ............. x= 7
13

Odp: boki trójkąta mają długości: 14, 13, 15

Franek: Geniusz nie podziękuje? No tak − geniusz.

Eta:

Geniusz: aaa dziękuje

Eta:

Nerd: Eta, byłbym wdzięczny gdybyś mogła rozjaśnić i dokładnie wytłumaczyć swój sposób rozwiązania