zad sylwia gdańsk: w tojkacie abc o bokach dlugosci ab=10 bc=9 ac=8 poprowadzono dwusieczne kata o wierzcholku a ktora podzielila bok bc punktem d na 2 czesci oblicz dlugosc otrzymanego odcinka

sylwia gdańsk: ?

sylwia gdańsk:

sylwia gdańsk: ok to mam

sylwia gdańsk: a nie nei kumam mam wzor a/b=c/d i co z tego?

Basia: Pomagam

Basia: CD+BD=BC CD+BD=8

CD		BD
	=
AC		AB

CD		BD
	=
8		10

	BD
CD=8*
	10

	4*BD
CD=
	5

4*BD
	+BD=8 /*5
5

4*BD+5*BD=40 9*BD = 40 BD=⁴⁰₉

	4*409
CD=
	5

CD=¹⁶⁰₄₅=³²₉

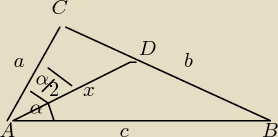
AS: Uwaga: Wierzchołki oznacza się literami dużymi,małe są zarezerwowane do oznaczania boków. Dane: AC = a = 8 , BC = b = 9 , AB = c = 10 , szukane AD = x PΔACD + PΔADB = PΔABC 1/2*a*x*sin(α/2) + 1/2*c*x*sin(α/2) = 1/2*a*c*sin(α) |*2 (a + c)*x*sin(α/2) = a*c*2*sin(α/2)*cos(α/2) a*c*cos(α/2) 80*cos(α/2) 40*cos(α/2) x = −−−−−−−−− = −−−−−−−−−− = −−−−−−− a + c 18 9 a² + c² − b² Z tw. cosinusów cos(α) = −−−−−−−−−− = 83/160 2*a*c Odczytać α z tablic,potem wyliczyć α/2 i wstawić do wzoru na x. Można by jeszcze policzyć dalej cos(α ) = cos²(α/2) − sin²(α/2) = cos²(α/2) − (1 − cos²(α/2) = 2*cos²(α/2) − 1 Stąd cos²(α/2) = (cos(α) + 1)/2 = 243/320 po podstawieniu cos(α) = 83/160 cos(α/2) = √243/320 = 9*√3/(8*√5) Podstawiając do x otrzymamy x = 40/9*9/8*√3/5 = 5*√3/5 = √15

sylwia gdańsk: dzieki

sylwia gdańsk: basia wiec co jest dobrze?

sylwia gdańsk: czemu masz CD+BD=8

AS: Basiu! Chyba popełniłaś błąd CD + DB = 9 Wtedy odcinki CD i DB wyniosą 4 i 5 i są w zgodzie z proporcją 4 :5 = 8 : 10

sylwia gdańsk: AS to mozna zorbic to jak basia bo ten twoj sposob mnie przeraza

sylwia gdańsk: BAsia ale co ty mi obliczylas?

Basia: Całkiem możliwe.

sylwia gdańsk: ja mialam wyliczyc AD tak naprawde

sylwia gdańsk: aha teraz z pitagorasa moge?

sylwia gdańsk: a nei przeciez to nie trojkat prostokatnyXD

sylwia gdańsk: jak mam obliczyc AD?

Basia: BD i CD, ale się pomyliłam bo BD+CD=BC=9 stąd BD=5 i CD=4 teraz wystarczy z tw.cosinusów w tr. ABC policzyć np.cosβ i za tw.cosinusów w tr.ABD policzyć AB liczenie kątów połówkowych jest wtedy zbędne

sylwia gdańsk: ale jak

AS: Sylwia! Jak Ciebie przeraża ten mój sposób,to można inaczej. Tw. cosinusów obliczyć kąty α , β i γ − bo trzy boki są dane. Potem z proporcji o dwusiecznej kąta AB : AC = BD : CD i BD + CD = BC znaleźć odcinek CD, wyniesie on 4 Teraz z ΔACD mając AC , CD i γ tw.cosinusów znaleźć AD.

sylwia gdańsk: i tak nei wiem o czym wy gadacie ale dizeki

Basia: AC² = AB²+BC²−2*AB*BC*cosβ 64 = 100+81−2*10*9*cosβ 180*cosβ=115 cosβ=¹¹⁷₁₈₀ AD² = AB²+BD²−2*AB*BD*cosβ AD² = 100+25−2*10*5*¹¹⁷₁₈₀ AD² = 125−^117*100₁₈₀=125−^117*10₁₈ = 125−^117*5₉ AD² = ^{125*9−117*5}₉ = ^{5(25*9−117)}₉ = ^5(225−117)₉ = ^5*108₉=5*12=60 AD = √60 = √4*15=2√15

sylwia gdańsk: dzieki

Basia: rachunki można uprościć bo cosβ=¹¹⁷₁₈₀ = ¹³₂₀ nie zauważyłam, że 117 dzieli się przez 9

AS: Poprawka do mego rozwiązania w wyrażeniu na x brakuje 2 Prawidłowo powinno być 2*a*c*cos(α/2) x = −−−−−−−−−−−−−− a + c i wynik końcowy 2*√15 Errare humanum est.

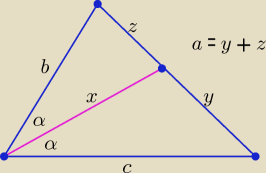
Bogdan: Jako ciekawostkę podaję wzory:

	ac		ab		a
y =		, z =		, x2 = bc(1 − (		)2 )
	b + c		b + c		b+c