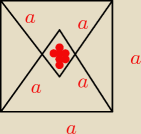
zad sylwia gdańsk: pole zamolowanego a=6

Basia: Pomagam

sylwia gdańsk: hehe

sylwia gdańsk: dzikei basiu za dobre checi

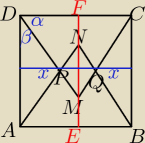
Basia: EM+MN+NF = a EM+MN = EN − wysokość tr.równobocznego o boku a

	a√3
EN =
	2

a√3
	+NF = a
2

	a√3		2a−a√3		a
NF = a−		=		=		*(2−√3)
	2		2		2

MN+NF=MF i to też jest wysokość trójkąta równobocznego o boku a EM=NF

	a
MN = a−2*		*(2−√3)
	2

MN = a−a(2−√3) = a−2a+a√3 = a√3−a = MN=a(√3−1) α=60 ⇒ β=30

	x
tgβ=
	a2

x = ^a₂*tg30

	a√3
x = a2*√33 =
	6

	a√3		3a−a√3
PQ = a−2x = a−		=
	3		3

PQ=^a₃*(3−√3)=^a₃*√3*(√3−1) P = ¹₂*MN*PQ podstaw i policz (i sprawdź czy się gdzieś w rachunkach nie pomyliłam)

sylwia gdańsk: pomozesz mi w innych tego typu?

Basia: No i podstaw za a to 6. Jakoś to przeoczyłam, ale nie szkodzi.

Basia: Jedno tam jeszcze podobne widziałam. Za chwilę do niego zajrzę.

sylwia gdańsk: to nei jest tr roznoboczny

tim: Nie, no nie jest No przecież jest

sylwia gdańsk: mi nauczyciel zostawil na to 1/2 kartki i podobno latwe a z tego co tu widze to masakra na bank nei ma latwiejszego sposobyu?

sylwia gdańsk: widze co mam namalowane

tim: Ja robiłem kiedyś podobne, spróbuję znaleźć.

tim: Ja też widzę ...

sylwia gdańsk: chyba ze nie jest dokladny heheh

tim: skoro AB = BC to ACBD jest kwadratem, a skoro DC = a, DM = a oraz CM = a, to jest to równoboczny.

sylwia gdańsk: to zmyla w takim razie xd nauczyciela

Basia: No przecież na rysunku wyraźnie jest pokazane, że te trójkąty są równoboczne.