Odległość pomiędzy łukami demo2012: Witam, mam taki oto problem: muszę obliczyć min. odległość w poziomie (ox) pomiędzy dwoma łukami (nie mylić z odległością między środkami). Znam współrzędne punkty środków łuków, ich promienie oraz kąty początku oraz końca. Punkty środków łuków mogą, ale nie muszą leżeć na prostej równoległej do osi ox. Z rozważań można wykluczyć przypadek, w którym łuki się przecinają. Jak się do tego zabrać?

Artur z miasta Neptuna: Poziom liceum czy studia albo inaczej ... pochodne znamy czy nie

demo2012: bez pochodnych

demo2012: Artur z miasta Neptuna ... i ..?

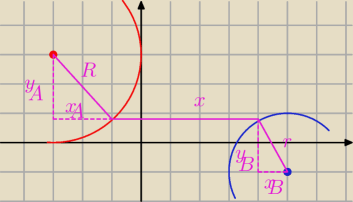Artur_z_miasta_Neptuna: założenie podstawowe: |SA_y − SB_y| < R+r <−−− różnica współrzędnych po 'y' mniejsza od sumy promieni łuków gdy niespełnione, to nie istnieje prosta równoległa do OX łącząca punkty tych dwóch łuków szczerze ... bez pochodnych jakoś nie widzę tego zadania skąd masz to zadanie ? Czyżby to nie było jakieś zadanie konkursowe

demo2012: dziękuję przynajmniej za próbę rozwiązania. Zadanie nie jest konkursowe pomiędzy pewnymi elementami w maszynie muszę mieć zachowaną pewną odległość i do tego muszę obliczyć aktualnie min po osi oX Twoje założenie oczywiście jest poprawne. Jeżeli bez pochodnych nie da rady to ... czy mógłbyś na dowolnym przykładzie (np. takim jak na rysunku) pokazać jak znaleźć rozwiązanie takiego zadania? Kiedyś miałem pochodne, więc po przypomnieniu sobie pewnie później dam radę zrobić to sam Z góry dziękuję.

Artur_z_miasta_Neptuna: nie ma problemu ... tylko daj mi chwilkę niestety będzie trochę warunków, ale samo zadanie nie powinno być ciężkie do rozwiązania (excel sobie poradzić powinien)

demo2012: ok, czekam z niecierpliwością

Artur z miasta Neptuna: Takie pytanie ... chcesz miec to rozpisane matematycznie czy moze byc jako funkcia minimum w excelu

demo2012: może być w excelu

Artur_z_miasta_Neptuna: szukając najkrótszej odległości równoległej do osi OX, pomiędzy łukami można rozpatrywać jako najkrótszą drogę pomiędzy środkami okręgów (ktorych promienie i współrzędne masz dane), gdzie droga jest tyczona w taki sposób jak pokazałem o 13:37. Odległość 'x' jest zmienna i zależy od x_A,y_A,x_B,y_B ... czyli 4 zmiennych. Jednak jest to spojrzenie niezwykle błędne ... bo tak naprawdę mamy do czynienia tylko z jedną zmienną ... ponieważ: x_A = √r²−y_A² y_A + y_B = |SA_y − SB_y| x_B = √r²−y_B² x = |SA_x − SB_x| − x_A − x_B = |SA_x − SB_x| − √R²−y_A² − √r²−y_B² = = |SA_x − SB_x| − √R²−y_A² − √r²−(|SA_y − SB_y| − y_A)² i masz minimalizować tą właśnie funkcję jednej zmiennej (y_A) z parametrami R,r, SA, SB przy pewnych warunkach: y_A, x_A, y_B, x_B muszą byc odpowiednio ograniczone ... aby reprezentowały współrzędne danego luku, a nie całego okręgu o danym środku i promieniu y_A ≥ |SA_y − SB_y| − r (warunek dolny na y_A) y_A ≤ R (warunek górny na y_A)

	yA		√|SAy − SBy| − yA
x' =		−
	√R2−yA2		r2−(|SAy − SBy| − yA)2

	R2|SAy − SBy| +/− Rr|SAy − SBy|
yA=		=
	R2−r2

	R|SAy − SBy|
=
	R +/− r

wyprowadzenia czysto teoretyczne −−− nie sprawdzałem na żadnych danych

demo2012: dobrze, dziękuję za to że poświęciłeś temu zadaniu tyle swojego czasu. Postaram się to dziś zaimplementować i sprawdzić na realnych danych. Jeszcze raz gorąco dziękuję za pomoc.

demo2012: Witam ponownie przepraszam, że to tak długo trwało ale ... mam wyniki moich doświadczeń. Wzór wydaje się być poprawny ale tylko w szczególnych przypadkach tzn. kiedy łuki są zwrócone do siebie "brzuszkami" czyli de facto obliczamy odległość pomiędzy okręgami. W innym przypadku niestety wzoru nie można zastosować. Poza tym otrzymujemy dwa różne wyniki przed i po uproszczeniu wzoru (ale to tylko mało istotny szczegół). Poniżej znajdują się dane "wejściowe" oraz wyniki: ya1 i ya2 to wyniki przed uproszczeniem ya11 i ya12 − po uproszczeniu Obliczenia robiłem z A do B oraz z B do A − dlatego są po dwa komplety dla każdego testu. W teście A prawidłowy wynik to 0.75432656089422134 oraz 0.9666157428395129 Kąty początku oraz końca łuku podawane są w radianach. TEST A START A.Centrum [0] 11.9402985074627 [1] 2.0870456221128482 [2] 0.0 A.Promień 3.6402861325252007 A.Alfa_Start 1.6629713643513582 A.Alfa_Stop 2.9537509431775097 B.Centrum [0] −1.750575680560428 [1] 3.8079879258465827 [2] 0.0 B.Promień 4.6647673124062985 B.Alfa_Start 5.33183419199273 B.Alfa_Stop 1.1861017007095918 ya1 −6.1150195105438394 ya2 0.75432656089422134 ya11 0.20721628285053489 ya12 −1.6798183680967851 ya1 7.8359618142775735 ya2 0.9666157428395129 ya11 0.20721628285053489 ya12 1.6798183680967851 TEST A STOP TEST B START A.Centrum [0] 14.270025596847695 [1] 2.0771144278608586 [2] 0.0 A.Promień 3.6402861325252007 A.Alfa_Start 0.18784171041229034 A.Alfa_Stop 1.4786212892384414 B.Centrum [0] 4.6647673124062994 [1] 3.7980567315945213 [2] 0.0 B.Promień 4.6647673124062985 B.Alfa_Start 1.955490952880236 B.Alfa_Stop 4.0929437687767249 ya1 −6.1150195105435845 ya2 0.75432656089418959 ya11 0.20721628285052621 ya12 −1.6798183680967149 ya1 7.8359618142772458 ya2 0.96661574283947282 ya11 0.20721628285052621 ya12 1.6798183680967149 TEST B STOP Problem teoretycznie jest prosty tylko jak go opisać? Będę wdzięczny za pomoc.

demo2012: odgrzewam temat

paula: pomozesz mi w zadaniu prosze

demo2012: nie ma na to mocnego?